虚拟变量可以代表质的因素,有些情况下,虚拟变量也可以代表数量因素。分段线性回归就是类似情形中常见的一种。
在经济关系中常有这样的情况:当解释变量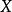 的值达到某一水平
的值达到某一水平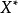 之前,与被解释变量
之前,与被解释变量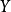 之间存在某种线性关系;当解释变量
之间存在某种线性关系;当解释变量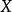 的值达到或超过
的值达到或超过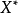 以后,与被解释变量的关系就会发生变化。此时,如果已知
以后,与被解释变量的关系就会发生变化。此时,如果已知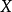 的转折点
的转折点 。我们就可以用虚拟变量来估计每一段的斜率。这就是所谓的分段线性回归2。
。我们就可以用虚拟变量来估计每一段的斜率。这就是所谓的分段线性回归2。
分段线性回归模型由两条直线组成,但在折点处曲线仍是连续的。考虑以下的基本模型:

假定因变量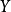 和解释变量
和解释变量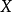 均呈现随时间稳定增长的趋势,在时间
均呈现随时间稳定增长的趋势,在时间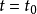 处反映两者之间关系的曲线出现转折,使得两段曲线的截距和斜率都发生变化,但
处反映两者之间关系的曲线出现转折,使得两段曲线的截距和斜率都发生变化,但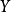 的变化具有连续性。我们设定以下形式的虚拟变量2:
的变化具有连续性。我们设定以下形式的虚拟变量2:
 然后将待估计的分段线性回归模型写成
然后将待估计的分段线性回归模型写成
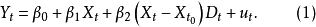
由式(1) 可以看出,当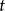 处于不同时间段时,
处于不同时间段时,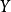 的期望值分别为
的期望值分别为
当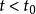 时,有
时,有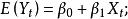
当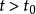 时,有
时,有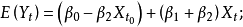
当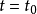 时,有
时,有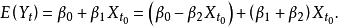
即在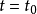 处曲线为连续的,图1反映出这一情况2。
处曲线为连续的,图1反映出这一情况2。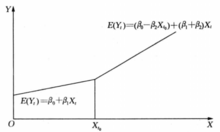
在研究实际经济问题时,有些经济变量之间的因果关系会在解释变量达到某个临界值时发生突变,为了区分这种变化,可以利用虚拟变量进行分段线性回归3。
例如,根据消费理论,消费水平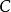 主要取决于收入水平
主要取决于收入水平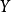 ;假设高收入与低收入人群的消费倾向存在差异,则这种消费倾向的差异可通过在收入的系数中引入虚拟变量来考察,建立如下消费模型:
;假设高收入与低收入人群的消费倾向存在差异,则这种消费倾向的差异可通过在收入的系数中引入虚拟变量来考察,建立如下消费模型:
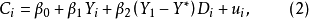 其中,
其中,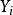 为收入水平,
为收入水平, 为划分高收入与低收入的临界值,
为划分高收入与低收入的临界值, 为消费水平,
为消费水平,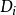 为虚拟变量,
为虚拟变量,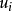 为随机扰动项。
为随机扰动项。
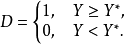 若模型(2)的随机扰动项满足经典线性回归模型的基本假设,则可以得到:
若模型(2)的随机扰动项满足经典线性回归模型的基本假设,则可以得到:
低收入人群
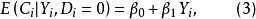
高收入人群
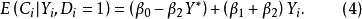
式(3)和式(4)分别表示低收入人群和高收入人群的消费函数;不同收入人群的消费行为是否存在显著差异,可以通过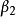 的统计显著性检验进行判断。
的统计显著性检验进行判断。
如图2所示,模型(2)实际上是将两段回归合并进行,这两段回归不仅截距不同,而且斜率不同。分两段线性回归引入了一个虚拟变量;容易推广,分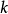 段线性回归应引入了
段线性回归应引入了 个虚拟变量3。
个虚拟变量3。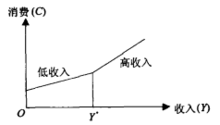




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国