下图是一个简单的确定汽车驾驶员风险的决策树(decision tree),使用这个树时,先考虑驾驶员的年龄。如果小于18岁,则考虑是否开红车,如果是,则认为该驾驶员是高风险的,否则是低风险的;如果年龄大于18岁,则考虑是否酗酒,如果是,则高风险,否则为低风险,当然,这个决策树仅仅是描述性的,比较简单。

这个决策树像一棵倒长的树(当然也可以横着放),变量年龄所在的节点称为根节点(root node),而底部的四个节点称为叶节点(leaf node)或终节点(terminal node)。这个树也称为分类树(classification tree),因为其目的是要把一个观测划分为“高风险“或“低风险”每个叶节点都是因变量的取值,而除了叶节点外的其他节点都是自变量。对于这个决策树,只要输人关于某司机的这几个变量的值,就立刻得到该司机相关的风险分类,
还有一种决策树是回归树(regression tree),其根节点为连续的因变量在这个分叉上的平均取值,分类树和回归树合起来也叫做CART(elassification andregression tree),上面的描述性决策树是二分的( binary split),即每个非叶节点(non-leaf node)刚好有两个叉。决策树也可有多分叉的(multi-way split) 。决策树的节点上的变量可能是各种形式的(连续、离散、有序、分类变量等),一个变量也可以重复出现在不同的节点,一个节点前面的节点称为其父节点(母节点或父母节点,parent node),而该节点为前面节点的子节点( 女节点或子女节点,child node),并列的节点也叫兄弟节点(姊妹节点,sibling node)。上面的例子是一棵现成的树,它不是随便画的,而是根据数据做出来的。
和经典回归不同,决策树不需要对总体进行分布的假定,而且,决策树对于预测很容易解释,这是其优点,此外,决策树很容易计算,但有必要设定不使其过分生长的停止规则或者修剪方法,决策树的一个缺点是每次分叉只和前一次分叉有关,而且并不考虑对以后的影响。因此,每个节点都依赖于前面的节点。如果开始的划分不同,结果也可能很不一样,目前有些人在研究分叉时考虑未来,但由于可能导致强度很大的计算,还没有见之于实际应用阶段1。
基本介绍决策树是一种从无次序、无规则的样本数据集中推理出决策树表示形式的分类规则方法。采用自上向下的递归方式,在决策树的内部节点进行属性值的比较,并根据不同属性值判断从该节点向下分,在决策树的叶结点得到结论。因此,从根节点到叶节点的一条路径就对应一条规则,整棵决策树就对应着一组表达式规则。比较典型的决策树算法是由Breiman于1984 年提出的分类回归树(CART,Classification and简称为CART分类树),并不断得到改进,现已在统计和Regression Trees,数据挖掘领域中普遍使用。它提供了一种非参数判别多数据层之间的统计关系,通过构建二叉树达到预测目的,采用一种二分递归分割的技术,将当前的样本集分为两个子样本集,使得生成的决策树的每个非叶子节点都有两个分支,其核心就是通过对由测试变量和目标变量构成的训练数据集的循环二分形成二叉树形式的决策树结构。CART分类树包含两个基本思想:第一是将练样本进行递归地划分自变量空间进行建树的想法;第二是用验证数据进行剪枝。
分裂标准分类错误率构建分类树和回归树在方法上大体相似,同回归树一样,用递归二元分裂法构建分类树。然而不同之处在于,残差平方和(RSS)不能作为二元分裂的标准,因此用分类错误率(Classification Error Rate)来替代残差平方和。由于我们的目的是用该区域内训练样本最可能发生的类别来推断观测值的归属,因此分类错误率指的就是训练样本没有被分入最可能发生的类别的比率,即:
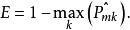 其中,
其中, 代表的是在第m个区域中来自第k个类别的训练样本所占的比重。然而分类错误率在构建分类树时效果欠佳,实践中更愿意使用后面两种方法2。
代表的是在第m个区域中来自第k个类别的训练样本所占的比重。然而分类错误率在构建分类树时效果欠佳,实践中更愿意使用后面两种方法2。
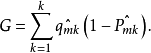
基尼系数(Gini Index)是对组间总方差的度量,当 趋于0或趋于1时,基尼系数值很小。对此,通常把基尼系数作为对节点纯度的度量——基尼系数小代表节点包含了来自某一单独类别的主要的观测值。
趋于0或趋于1时,基尼系数值很小。对此,通常把基尼系数作为对节点纯度的度量——基尼系数小代表节点包含了来自某一单独类别的主要的观测值。

由于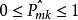 ,所以,
,所以,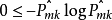 。同样当
。同样当 趋于0或趋于1时,交叉熵(Cross-entropy)很小,接近于0。因此,同基尼系数一样,交叉熵的值很小时代表节点的纯度高。事实上,基尼系数和交叉熵在数值上是十分相似的。
趋于0或趋于1时,交叉熵(Cross-entropy)很小,接近于0。因此,同基尼系数一样,交叉熵的值很小时代表节点的纯度高。事实上,基尼系数和交叉熵在数值上是十分相似的。
因为基尼系数和交叉熵相比于分类错误率对节点的纯度更敏感,所以在构建分类树的时候,通常使用基尼系数或是交叉熵来评价某一分裂的质量。然而在修剪分类树时,尽管三种方法都可以使用,但是如果修剪分类树的目的是提高预测精度,那么分类错误率的指标更好2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国