[科普中国]-回归正交设计

回归正交设计是广泛应用的回归设计方法，它主要基于正交试验的优点(按正交原则安排试验点称为正交试验)，利用正交表来安排试验。如果试验点是等间距的，那么就可以按正交多项式进行回归计算，这种计算由于去掉了各因素间的相关性，同时系数矩阵又可以化为对角阵，因此大大简化了回归计算的工作量。但是应该指出的是，在安排试验点时不仅应考虑试验点的正交性，而且根据这个特点安排试验应能达到以最合理的试验点寻求生产工艺的最优化区域，然后在这个区域内建立数学模型的目的。这样把试验安排与试验数据的回归计算统一考虑，就能做到试验点少但合理、试验数据分布可靠，计算简单，回归方程精度高。按正交多项式回归模型中自变量的方次来分，回归设计按类型分为回归的正交设计、旋转设计、最优设计、均匀设计以及混料设计等；按次数又分为一次回归正交设计和二次回归正交设计。高于二次的正交设计用得较少。

一次回归正交设计是指表达试验结果的回归方程只有常数项、线性项和线性交互作用项，其回归模型为：

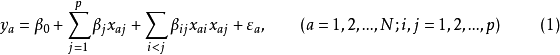
多数情况下是利用二水平正交表安排多因素试验，各因素水平上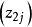限及下限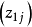确定后取线性变换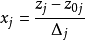对实际水平进行编码，其中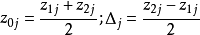。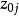称为零水平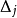，称为变化区间，是编码值为1的水平间距。经线性变换二水平正交表中的1、2 两个水平都转化为编码值-1及1两个无量纲的纯数。各因素不同水平的取值可能大小不一，转化为-1及1两个水平编码值后即成为多维正立方体因子空间。对回归模型(1)，令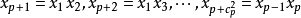，则模型(1)转化为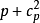阶线性回归模型。

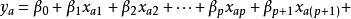
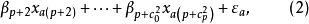式(2)中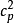为p个元素中取2个的组合数，就是两因素,交互作用的项数、如将两因素交互作用也理解为1个因素，并将其包括在p个因素之内，则式(2)可简化表示为

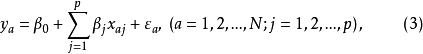由于式(3)的结构矩阵X如下，它由试验方案各处理的水平组合所决定。

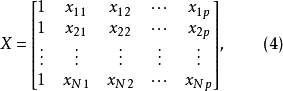其中各项因素均经过线性变换为-1及1两个水平编码值，除常数项的系数为1外，其余各列均符合正交条件，所以参数β的最小二乘估计b可简化为

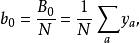
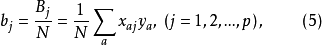的回归方程为

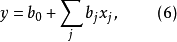正交性已消除了结构矩阵中各列之间的相关性，故可剔除不显著的项2。

二次回归正交设计是指回归模型中包括常数项、线性项、线性交互作用项及二次项的回归正交设计，回归模型为：

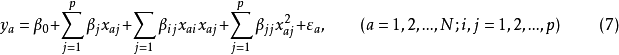各个因素的水平数必须多于3个才可求出式(7)中的二次项。为了精确绘出二次曲线，常须进行5个水平的试验，这时处理组合数将多到无法实施，解决这个困难的方法是组合设计。组合设计各实验单元的处理内容由三部分组成：①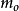。为二水平正交表中各处理组合。②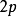。为分布于p个因素坐标轴上距中心点距离为γ的轴点，称为星号臂。③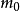。各因素都取零水平的中心点。

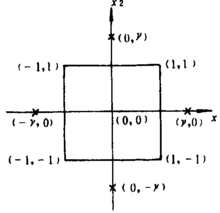
二因素及三因素试验各处理组合在因子空间中的分布如图1、2。

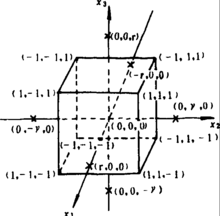
可取不同重复次数，处理组合数目N为

组合设计有5个水平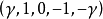，但处理组合数目比完全实施方案少得多，从而减少过多的剩余自由度。

为了使式(7)结构矩阵符合正交条件采取了二个措施:①用公式调整星号臂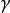

取值；②对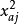列进行中心化变换，得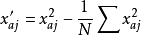。当试验的因素数及各因素水平上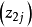限及下限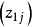确定后，即可用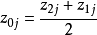对试验水平编码，与一次回归正交设计不同的是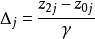。经以上处理后式(7) 成为式(9)

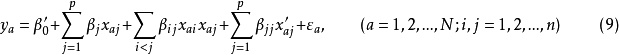式(9)的结构矩阵内各列符合正交条件，参数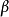的最小二乘估计b 由式(10) 求得:

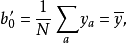
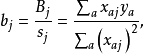
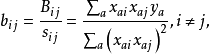
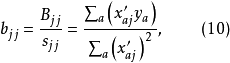得回归方程为：

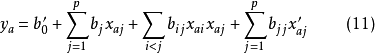将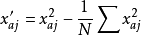代入式（11），即得回归方程的一般形式

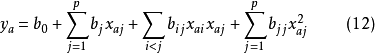对式(11)进行显著性检验后，即可按部分处理有重复的方差分析，再在因子空间中寻优。

回归正交设计的突出优点是可以用很少的处理组合得出完全实施试验相同项数的回归模型，计算过程极为简单并已消除了回归系数之间的相关性，统计性质得到了明显改善，因此在计算机推荐施肥的多因素肥料试验中应用甚广2。