基本介绍
单变量统计分析可以分为两个大的方面,即描述统计和推论统计。描述统计的主要目的在于用最简单的概括形式反映出大量数据资料所容纳的基本信息。它的基本方法包括集中趋势分析、离散趋势分析等。而推论统计则是用从样本中所得到的数据资料来推断总体的情况,它主要包括区间估计和假设检验等1。
单变量描述统计集中趋势分析集中趋势分析指的是用一个典型值或代表值来反映一组数据的一般水平,或者说反映这组数据向这个典型值集中的情况。最常见的集中趋势有算术平均数(简称平均数,也称为均值)、众数和中位数3种。这里只对使用最多的平均数略作介绍。平均数的定义是:总体各单位数值之和除以总体单位数目之商。统计分析中习惯用来表示。其计算公式如下:
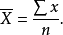
如果是单值分组资料,那么,计算平均数时首先要将每一个变量值乘以所对应的频数f,然后将各组的数值之和全部相加,并除以单位总数(也即各组频数之和)。其公式是:
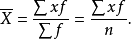
在调查收人、年龄等方面情况时,常常得到组距分组形式的资料(比如,人口普查的许多数据就是以年龄分组的形式给出的,即我们常常知道的是0~4岁,5~9岁、10~14岁等年龄段的人数、他们的各种特征等)。这时,若要计算样本的平均数,就需要先计算出各组的组中值,然后再按照上述单值分组资料计算平均数的公式计算。组中值的计算公式为:组中值=(上限+下限)/2。
当组中值为小数时,通常采取四舍五人的办法将其化为整数后再计算。
离散趋势分析与集中趋势分析相反,离散趋势分析指的是用一个特别的数值来反映一组数据相互之间的离散程度。它与集中趋势一起,分别从两个不同的侧面描述和揭示一组数据的分布情况,共同反映出资料分布的全面特征。同时,它还对相应的集中趋势(如平均数、众数、中位数)的代表性作出补充说明。
常见的离散趋势统计量有全距、标准差、异众比率、四分位差等。其中,标准差、异众比率、四分位差分别与平均数、众数、中位数相对应,判定和说明平均数、众数、中位数代表性的大小。下面我们主要介绍标准差和离散系数。
标准差的定义是:一组数据对其平均数的偏差平方的算术平均数的平方根。它是用得最多、也是最重要的离散趋势统计量,其计算公式为:
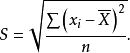
对于单值分组数据资料,计算标准差的公式略有变化:
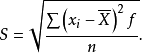 其中,
其中,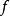 为
为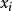 所对应的频数。由组距分组资料计算标准差时,只需先计算出各组的组中值,然后按照单值分组资料计算标准差的公式和方法计算即可。离散系数是一种相对的离散趋势统计量,它使我们能够对同一总体中的两种不同的离散趋势统计量进行比较,或者对两个不同总体中的同一离散趋势统计量进行比较。离散系数的定义是:标准差与平均数的比值用百分比表示。其计算公式为1:
所对应的频数。由组距分组资料计算标准差时,只需先计算出各组的组中值,然后按照单值分组资料计算标准差的公式和方法计算即可。离散系数是一种相对的离散趋势统计量,它使我们能够对同一总体中的两种不同的离散趋势统计量进行比较,或者对两个不同总体中的同一离散趋势统计量进行比较。离散系数的定义是:标准差与平均数的比值用百分比表示。其计算公式为1:
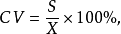 (CV 为离散系数).
(CV 为离散系数).
单变量推论统计简单地说,推论统计就是利用样本的统计值对总体的参数值进行估计的方法。推论统计的内容主要包括两个方面:一是区间估计;二是假设检验。
区间估计区间估计的实质就是在一定的可信度(置信度) 下,用样本统计值的某个范围(置信区间)来估价总体的参数值。范围的大小反映的是这种估计的精确性问题,而可信度高低反映的则是这种估计的可靠性或把握性问题。区间估计的结果通常可以采取下述方式来表述:“我们有95%的把握认为,全市职工的月工资收入在182-218元之间”。或者“全省人口中,女性占50%~52%的可能性为99%”。
区间估计中的可靠性或把握性是指用某个区间去估计总体参数时,成功的可能性有多大。它可以这样来解释:如果从总体中重复抽样100次,约有95次所抽样本的统计值的某个区间中都将包含总体的参数值,那么就说这个区间估计的可靠性为95%,对于同一总体和同一抽样规模来说,所给区间的大小与作出这种估计所具有的把握性呈正比,即所估计的区间越大,则对这一估计成功的把握性也越大;反之,则把握性越小。实际上,区间的大小所体现的是估计的精确性问题,上者呈反比,即区间越大,精确程度越低;区间越小,精确程度越高。从精确性出发,要求所估计的区间越小越好;但从把握性出发,又要求所估计的区间越大越好。因此,人们总是需要在这二者之间进行平衡和选择。在社会统计分析中,常用的置信度分别为90%,95%和99%,与它们所对应的允许误差(a)则分别为10%,5%和1%。在计算中,置信度常用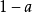 来表示。下面我们分别介绍总体均值和总体百分数的区间估计方法。
来表示。下面我们分别介绍总体均值和总体百分数的区间估计方法。
(1)总体均值的区间估计
总体均值的区间估计公式为:
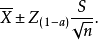 其中,
其中,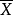 为样本平均数;S为样本标准差;
为样本平均数;S为样本标准差;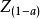 叫为置信度是
叫为置信度是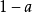 的
的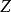 值;
值; 为样本规模。
为样本规模。
(2)总体百分数的区间估计
总体百分数的区间估计公式为:
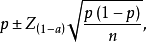 这里,
这里,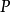 为样本中的百分比。
为样本中的百分比。
假设检验假设检验问题是推论统计中的另一种类型。首先需要说明的是,这里的假设不是指抽象层次的理论假设,而是指和抽样手段联系在一起并且依靠抽样数据进行验证的经验层次的假设,即统计假设。
假设检验,实际上就是先对总体的某一参数作出假设,然后用样本的统计量去进行验证,以决定假设是否为总体所接受。假设检验所依据的是概率论中的小概率原理,即“小概率事件在一次观察中不可能出现”的原理。但是,如果现实的情况恰恰是在一次观察中小概率事件出现了,那该如何判断呢?一种是认为该事件的概率仍然很小,只不过不巧被碰上了;另- 一种则是怀疑和否定该事件的概率未必很小,即认为该事件本身不是一种小概率事件,而是一种大概率事件。后一种判断更为合理,它所代表的正是假设检验的基本思想。概括起来,假设检验的步骤是:
(1) 建立虚无假设和研究假设。通常是将原假设作为虚无假设。
(2) 根据需要选择适当的显著性水平a(即概率的大小),通常有a=0.05,a=0.01等。
(3) 根据样本数据计算出统计值,并根据显著性水平查出对应的临界值。
(4) 将临界值与统计值进行比较,若临界值大于统计值的绝对值,则接受虚无假设;反之,则接受研究假设1。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国