基本概念
指数平滑法的计算公式为:
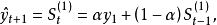 式中,
式中, 为平滑系数;
为平滑系数;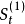 为
为 时刻的一次指数平滑值;
时刻的一次指数平滑值;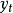 为
为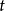 时刻的实际值1。
时刻的实际值1。
指数平滑法指数平滑法(exponential smoothing,ES)又叫指数修匀法,是由布朗(Robert G.Brown)所提出的。布朗认为,时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到未来,所以将较大的权数放在最近的资料。指数修匀法是预测中常用的一种方法,也用于中短期经济发展趋势预测,所有预测方法中,一次指数修匀法是用得最多的一种。简单的全期平均法是对时间数列的过去数据个不漏地全部加以同等利用;移动平均法则不考虑较远期的数据,并在加权移动平均法中给予近期资料更大的权重;而指数修匀法则兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。也就是说指数修匀法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均1。
平滑系数选择的原则平滑系数选择的原则:
(1)如果时间序列波动不大,比较平稳,则平滑系数应取小一点,以减少修正幅度,使预测模型能包含较长时间序列的信息。
(2)如果时间序列具有迅速且明显的变动倾向,则平滑系数应取大一点,以使预测模型灵敏度高些,以便迅速跟上数据的变化。
(3)在实用中,可多取几个值进行试算,取使预测误差较小的平滑系数。
初始值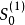 的确定
的确定
一般依据资料项数n的大小而定。
(1)当时间序列的数据n




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国