曲线相关是相对于线性相关而言的,也称为非线性相关,即相关的现象之间的相关形式并不表现为直线的关系,而是近似于某种曲线的关系。社会经济领域有许多现象之间的关系表现为非线性相关。对非线性相关的现象之间的回归分析称为非线性回归分析,或曲线回归分析。在只涉及一个自变量的情况下,称两个变量之间的回归为一元非线性回归。非线性回归分析必须着重解决以下两个问题:第一,如何确定非线性函数的具体形式。
与线性回归分析的场合不同,非线性回归函数有多种多样的具体形式,需要根据所要研究的问题的性质并结合实际的样本观测值做出恰当的选择。第二。如何估计函数中的参数。非线性回归分析最常用的方法仍然是最小二乘估计法。但需要根据函数的不同类型做出适当的处理1。
曲线回归方程的主要函数形式抛物线形回归方程为:
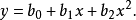
双曲线函数有多种形式,这里只介绍其中的一种:
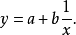
若 和
和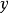 都接近等比变化,可配合幂函数曲线。其方程为
都接近等比变化,可配合幂函数曲线。其方程为
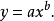
指数曲线的函数为

对数曲线的方程式为
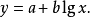
一元非线性回归的问题,大多可以转化为线性回归问题来解决,也就是通过对非线性回归模型进行适当的变量变换,使其转化为线性模型来求解。以下介绍几种常用的线性变换方法。
倒数变换倒数变换是用新的变量来替换原模型中变量的倒数,从而使模型变成线性模型的一种方法。例如,对于双曲线函数,令 代人原方程式,则有
代人原方程式,则有
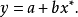
对数变换主要用于对数函数的线性变换。对于对数函数,令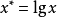 ,代人原方程,可得
,代人原方程,可得
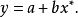
如对指数曲线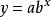 ,等号两边分别取对数,得
,等号两边分别取对数,得
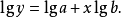 令:
令: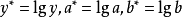 ,则方程转化为
,则方程转化为
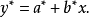
多项式变换适用于多项式方程的变换。例如,对抛物线方程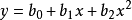 ,令
,令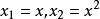 ,则有
,则有
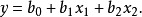
由相关系数的含义可知,相关系数用于测度现象间线性相关程度的大小。而对于变量之间存在曲线相关的强弱,难以用单相关系数去作正确的判断。在这种场合下,可以利用相关指数,作为判断变量之间是否存在某种类型的非线性相关关系的尺度。所谓相关指数,也就是对非线性回归模型进行拟合时所得到的可决系数。相关指数用R表示,其公式如下1:
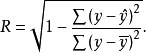
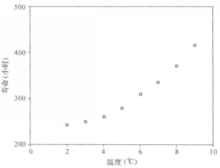
已知某种产品使用寿命与加工温度的一组数据如表1所示。试配合一条回归曲线。
表1 产品使用寿命与加工温度相关资料| 加工温度(℃) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 使用寿命(小时) | 242 | 250 | 260 | 280 | 310 | 335 | 370 | 415 | |
解:从散点图(见图1)可以看出,产品的使用寿命与加工温度的关系近似地表现为一条指数曲线: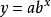 。
。
对方称两边取对数: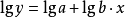 ,
,
令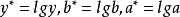 ,则
,则
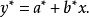 按直线回归的方法求参数
按直线回归的方法求参数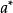 及
及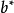 ,计算结果如表2所示。
,计算结果如表2所示。
| 序号 | x | y* | x2 | xy* |
| 1 | 2 | 2.3838 | 4 | 4.76763 |
| 2 | 3 | 2.3979 | 9 | 4.19382 |
| 3 | 4 | 2.4150 | 16 | 9.65989 |
| 4 | 5 | 2.4472 | 25 | 12.23579 |
| 5 | 6 | 2.4914 | 36 | 14.94817 |
| 6 | 7 | 2.5250 | 49 | 17.67531 |
| 7 | 8 | 2.5682 | 64 | 20.54561 |
| 8 | 9 | 2.6180 | 81 | 23.56243 |
| 合计 | 44 | 19.84654 | 284 | 110.58866 |
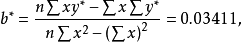
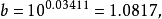
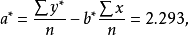
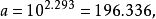
所以,产品寿命对加工温度的曲线回归方程为1
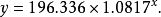




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国