开映射定理有一些重要的结果1:
1.如果 是巴拿赫空间X和Y之间的双射连续线性算子,那么逆算子
是巴拿赫空间X和Y之间的双射连续线性算子,那么逆算子 也是连续的。(Rudin 1973, 推论2.12) ;
也是连续的。(Rudin 1973, 推论2.12) ;
2.如果 是巴拿赫空间X和Y之间的线性算子,且如果对于X内的每一个序列(
是巴拿赫空间X和Y之间的线性算子,且如果对于X内的每一个序列( ),只要xn → 0且
),只要xn → 0且 就有
就有 ,那么A就是连续的(闭图像定理)。(Rudin 1973, 定理2.15)。
,那么A就是连续的(闭图像定理)。(Rudin 1973, 定理2.15)。
我们需要证明,如果 是巴拿赫空间之间的连续线性满射,那么
是巴拿赫空间之间的连续线性满射,那么 就是一个开映射。为此,只需证明
就是一个开映射。为此,只需证明 把
把 内的单位球映射到
内的单位球映射到 的原点的一个邻域。
的原点的一个邻域。
设 分别为
分别为 和
和 内的单位球。那么
内的单位球。那么 是单位球的倍数
是单位球的倍数 的序列的交集,
的序列的交集, ,且由于
,且由于 是满射,
是满射,

根据贝尔纲定理,巴拿赫空间 不能是可数个无处稠密集的并集,故存在
不能是可数个无处稠密集的并集,故存在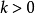 ,使得
,使得 的闭包具有非空的内部。因此,存在一个开球
的闭包具有非空的内部。因此,存在一个开球 ,其中心为
,其中心为 ,半径
,半径 ,包含在
,包含在 的闭包内。如果
的闭包内。如果 ,那么
,那么 和
和 位于
位于 内,因此是
内,因此是 的极限点,根据加法的连续性,它们的差
的极限点,根据加法的连续性,它们的差 是
是 的极限点。根据A的线性,这意味着任何
的极限点。根据A的线性,这意味着任何 都位于
都位于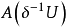 的闭包内,其中
的闭包内,其中 。于是可以推出,对于任何
。于是可以推出,对于任何 和任何
和任何 ,都存在某个
,都存在某个 ,满足:
,满足:
 且
且 (1)
(1)
固定 。根据(!),存在某个
。根据(!),存在某个 ,满足
,满足 且
且 ||y−A x 1||
||y−A x 1||




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国