定义
无穷积分
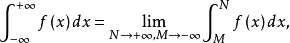 的定义,如换成
的定义,如换成
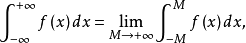 则称此积分为柯西主值。
则称此积分为柯西主值。
类似地,在瑕积分的定义中,设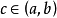 ,若
,若
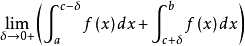 存在,则称瑕积分
存在,则称瑕积分
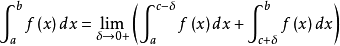 为柯西主值。1
为柯西主值。1
应用在物理学中有Kramers–Kronig定理,就是说响应和耗散分别是一个函数的实部和虚部,他们之间由一个柯西主值积分相联系。实验上一般测量响应或者耗散的其中一个,然后按Kramers–Kronig定理积分取柯西主值就可以得到另一个。这里的积分是不能收敛的,如果不取柯西主值,物理学家就无法进行下一步。
定义
无穷积分
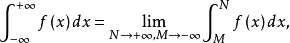 的定义,如换成
的定义,如换成
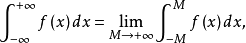 则称此积分为柯西主值。
则称此积分为柯西主值。
类似地,在瑕积分的定义中,设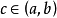 ,若
,若
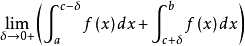 存在,则称瑕积分
存在,则称瑕积分
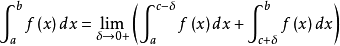 为柯西主值。1
为柯西主值。1
应用在物理学中有Kramers–Kronig定理,就是说响应和耗散分别是一个函数的实部和虚部,他们之间由一个柯西主值积分相联系。实验上一般测量响应或者耗散的其中一个,然后按Kramers–Kronig定理积分取柯西主值就可以得到另一个。这里的积分是不能收敛的,如果不取柯西主值,物理学家就无法进行下一步。
 扫码下载APP
扫码下载APP

