过去一百多年,一阶逻辑出现过许多种名称,包括:一阶断言演算、低阶断言演算、量化理论或断言逻辑(一个较不精确的用词)。一阶逻辑和命题逻辑的不同之处在于,一阶逻辑有使用量化变数。一个一阶逻辑,若具有由一系列量化变数、一个以上有意义的断言字母及包含了有意义的断言字母的纯公理所组成的特定论域,即是一个一阶理论。
一阶逻辑和其他高阶逻辑不同之处在于,高阶逻辑的断言可以有断言或函数当做引数,且允许断言量词或函数量词的(同时或不同时)存在。在一阶逻辑中,断言通常和集合相关连。在有意义的高阶逻辑中,断言则会被解释为集合的集合。
存在许多对一阶逻辑是可靠(所有可证的叙述皆为真)且完备(所有为真的叙述皆可证)的演绎系统。虽然一阶逻辑的逻辑归结只是半可判定性的,但还是有许多用于一阶逻辑上的自动定理证明。一阶逻辑也符合一些使其能通过证明论分析的元逻辑定理,如勒文海姆–斯科伦定理及紧致性定理。
一阶逻辑是数学基础中很重要的一部分,因为它是公理系统的标准形式逻辑。许多常见的公理系统,如一阶皮亚诺公理和包含策梅洛-弗兰克尔集合论的公理化集合论等,都可以形式化成一阶理论。然而,一阶定理并没有能力去完整描述及范畴性地建构如自然数或实数之类无限的概念。这些结构的公理系统可以由如二阶逻辑之类更强的逻辑来取得。
概念不像命题逻辑只处理简单的陈述命题,一阶逻辑还额外包含了断言和量化。
断言像是一个会传回真或伪的函数。考虑下列句子:“苏格拉底是哲学家”、“柏拉图是哲学家”。在命题逻辑里,上述两句被视为两个不相关的命题,简单标记为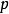 及
及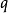 。然而,在一阶逻辑里,上述两句可以使用断言以更相似的方法来表示。其断言为
。然而,在一阶逻辑里,上述两句可以使用断言以更相似的方法来表示。其断言为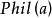 ,表示
,表示 是哲学家。因此,若
是哲学家。因此,若 代表苏格拉底,则
代表苏格拉底,则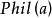 为第一个命题-
为第一个命题-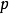 ;若
;若 代表柏拉图,则
代表柏拉图,则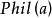 为第二个命题-q。一阶逻辑的一个关键要点在此可见:字串“
为第二个命题-q。一阶逻辑的一个关键要点在此可见:字串“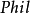 ”为一个语法实体,以当
”为一个语法实体,以当 为哲学家时陈述
为哲学家时陈述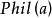 为真来赋与其语义。一个语义的赋与称为解释。
为真来赋与其语义。一个语义的赋与称为解释。
一阶逻辑可分成两个主要的部分:语法决定哪些符号的组合是一阶逻辑内的合法表示式,而语义则决定这些表示式之前的意思。
词汇表和英语之类的自然语言不同,一阶逻辑的语言是完全形式的,因为可以机械式地判断一个给定的表示式是否合法。存在两种合法的表示式:“项”(直观上代表物件)和“公式”(直观上代表可真或伪的断言)。一阶逻辑的项与公式是一串符号,这些符号一起形成了这个语言的词汇表。如同所有的形式语言一般,符号本身的性质不在形式逻辑讨论的范围之内;它们通常只被当成字母及标点符号。
一般会将词汇表中的符号分成“逻辑符号”(总有相同的意思)及“非逻辑符号”(意思依解释不同而变动)。例如,逻辑符号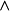 总是解释成“且”,而绝不会解释成“或”。另一方面,一个非逻辑断言符号,如Phil(x) ,可以解释成“x是哲学家”、“x的个名为Phil的人”或任何其他的1元断言,单看其解释为何。
总是解释成“且”,而绝不会解释成“或”。另一方面,一个非逻辑断言符号,如Phil(x) ,可以解释成“x是哲学家”、“x的个名为Phil的人”或任何其他的1元断言,单看其解释为何。
词汇表中存在若干个逻辑符号,虽然会因作者而异,但通常包括:
1) 量化符号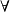 及
及 。
。
2)逻辑联结词:且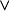 、或
、或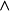 、条件
、条件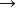 、双条件
、双条件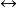 及否定
及否定 。偶尔还会包括一些其他的逻辑联结词。
。偶尔还会包括一些其他的逻辑联结词。
3) 括号、方括号及其他标点符号。此类符号的选择依文章不同而有所不同。
4) 无限集的变数,通常标记为英文字母末端的小写字母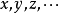 ,也常会使用下标来区别不同的变数:
,也常会使用下标来区别不同的变数: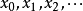 。
。
5)一个等式符号= 。详见下面的“等式”一节。
需注意,并不是所有的符号都需要,只要有量化符号的其中一个、否定及且、变数、括号及等式就足够了。还存在许多定义了额外逻辑符号的变体:
6)有时也会包括真值常数,用T、Vpq或 来表示“真”,并用F、Opq或
来表示“真”,并用F、Opq或 来表示“假”。若没有此类零参数的逻辑算符,这两个常数就只能用量化来表示。
来表示“假”。若没有此类零参数的逻辑算符,这两个常数就只能用量化来表示。
7)有时也会包括额外的逻辑联结词,如谢费尔竖线、NAND及异或。
2.非逻辑符号非逻辑符号用来表示论域上的断言(关系)、函数及常数。以前标准上会对所有不同的用途使用相同的无限集的非逻辑符号,而最近则会根据应用的不同而使用不同的非逻辑符号。因此变得需要列举出使用于一特定应用中的所有非逻辑符号。其选择是经由标识来形成的。
传统的做法是对所有的应用都只有单一个无限集的非逻辑符号。因此,根据传统的做法只会存在一种一阶逻辑的语言。这种做法现在依然很常见,尤其是在哲学方面的书籍。
1)对每个整数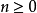 ,皆存在一组
,皆存在一组 元断言符号。因为这些断言符号表示
元断言符号。因为这些断言符号表示 个元素间的关系,因此也称为关系符号。对每个参数量
个元素间的关系,因此也称为关系符号。对每个参数量 ,皆能有无限多个断言符号:
,皆能有无限多个断言符号: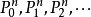
2)对每个整数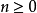 ,皆存在无限多个
,皆存在无限多个 元函数符号:
元函数符号: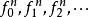
在当代的数理逻辑里,标识会因应用的不同而不同。数学里的典型标识,在群里为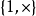 或只为
或只为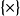 ;在序体里为
;在序体里为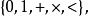 。并没有限制非逻辑符号的数量,标识可以是空的、有限、无限,甚至是不可数的。例如,在勒文海姆–斯科伦定理的证明之中即会出现不可数的标识1。
。并没有限制非逻辑符号的数量,标识可以是空的、有限、无限,甚至是不可数的。例如,在勒文海姆–斯科伦定理的证明之中即会出现不可数的标识1。
生成规则定义一阶逻辑的项及公式。因为项及公式被表示为一串符号,这些规则可被用来写成项及公式的形式文法。这些规则通常是上下文无关的(规则的每个结果在其左侧都会有单一个符号),除非允许有无限多符号,且有许多开始符号,如项中的变数。
1.项项可依如下规则递归地定义:
1.变数:每个变数皆是项。
2.函数:每个具有 个参数的表示式
个参数的表示式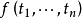 ,其中每个参数
,其中每个参数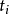 是项,且
是项,且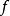 是具有
是具有 个参数的函数符号)是项。另外,常数符号是0参数的函数符号,因此也是项。
个参数的函数符号)是项。另外,常数符号是0参数的函数符号,因此也是项。
只有可经由有限次地应用上述规则来得到的表示式才是项。举例来说,不存在包含断言符号的项。
2.合成公式合式公式可依如下规则递归地定义:
1)断言符号:若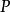 是一个n元断言符号,且
是一个n元断言符号,且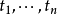 是项,则
是项,则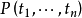 是公式。
是公式。
2)等式:若等式符号算是逻辑的一部分,且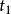 及
及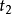 是项,则
是项,则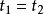 是公式。
是公式。
3)否定:若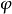 是公式,则
是公式,则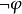 是公式。
是公式。
4)二元联结词:若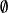 及
及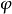 是公式,则
是公式,则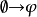 是公式。其他的二元逻辑联结词也可相似的规则。
是公式。其他的二元逻辑联结词也可相似的规则。
5)量化:若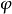 是公式,且
是公式,且 是变数,则
是变数,则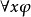 及
及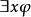 都是公式。
都是公式。
只有可经由有限次地应用上述规则来得到的表示式才是公式。由头两个规则得到的公式称为原子公式。
举例来说,
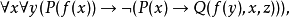 是公式,若
是公式,若 是1元函数符号,
是1元函数符号,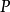 是1元断言符号,且
是1元断言符号,且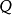 是3元断言符号。另一方面,
是3元断言符号。另一方面,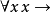 则不是公式,虽然这也是由词汇表中的符号组成的字串。
则不是公式,虽然这也是由词汇表中的符号组成的字串。
定义中的括号,其用途是为了确保任何公式都只能依递归定义以单一种方法得到(换句话说,每一个公式都只存在唯一的剖析树)。这个性质被称为公式的唯一可读性。对于括号要用在公式中的哪里存在有许多的惯例。例如,有些作者会使用冒号或句号来代替括号,或变更括号插入的地方。但每个作家个人的定义都必须证明会满足唯一可读性。
定义公式的规则无法定义“若-则-否则”函数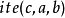 ),其中的
),其中的 是个以公式表示的条件,当
是个以公式表示的条件,当 为真时传回
为真时传回 ,为假时传回
,为假时传回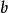 。这是因为断言和函数都只能接受项当做其参数,但上述函数的第一个参数为公式。某些建构在一阶逻辑上的语言,如SMT-LIB 2.0,会增加此一定义。
。这是因为断言和函数都只能接受项当做其参数,但上述函数的第一个参数为公式。某些建构在一阶逻辑上的语言,如SMT-LIB 2.0,会增加此一定义。
肯定前件充当推理的唯一规则。叫做全称普遍化的推理规则是断言演算的特征。它可以陈述为:
如果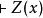 ,则
,则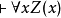 。
。
这里的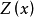 假定表示断言演算的一个已证明的定理,而
假定表示断言演算的一个已证明的定理,而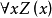 是它针对于变量x的闭包。断言字母Z可以被任何断言字母所替代。
是它针对于变量x的闭包。断言字母Z可以被任何断言字母所替代。
下面描述一阶逻辑的公理。如上所述,一个给定的一阶理论有进一步的非逻辑公理。下列逻辑公理刻画了本文的样例一阶逻辑的一种演算。
对于任何理论,知道公理的集合是否可用算法生成,或是否存在算法确定合式公式为公理,是很有价值的。
如果存在生成所有公理的算法,则公理的集合被称为递归可枚举的。
如果存在算法在有限步骤后确定一个公式是否是公理,则公理的集合被称为递归的或“可判定的”。在这种情况下,你还可以构造一个算法来生成所有的公理:这个算法简单的(随着长度增长)一个接一个的生成所有可能的公式,而算法对每个公式确定它是否是个公理。
一阶逻辑的公理总是可判定的。但是在一阶理论中非逻辑公式就不必需如此。
1.量词公理下列四个公理是断言演算的特征:
1. PRED-1: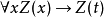 ,
,
2. PRED-2: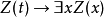 ,
,
3. PRED-3: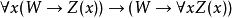 ,
,
4. PRED-4: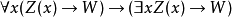 。
。
它们实际上是公理模式:表达式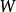 表示对于其中任何
表示对于其中任何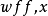 不是自由的;而表达式
不是自由的;而表达式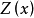 表示对于任何
表示对于任何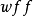 带有额外的约定,即
带有额外的约定,即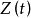 表示把
表示把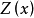 中的所有
中的所有 替代为项
替代为项 的结果。
的结果。
在一阶逻辑中对使用等式(或恒等式)有多种不同的约定。本节总结其中主要的。不同的约定对同样的工作给出本质上相同的结果,区别主要在术语上。
1.对等式的最常见的约定是把等号包括为基本逻辑符号,并向一阶逻辑增加等式的公理。等式公理是
1)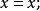
2) 对于任何函数 ,
,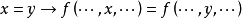 ;
;
3)对于任何关系P(包括 = 自身),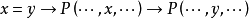
2.其次常见的约定是把等号包括为理论的关系之一,并向这个理论的公理增加等式的公理。在实际中这是同前面约定最难分辨的,除了在没有等式概念的不常见情况下。公理是一样的,唯一的区别是把它叫做逻辑公理还是这个理论的公理。
3.在没有函数和有有限数目个关系的理论中,有可能以关系的方式定义等式,通过定义两个项s和t是相等的,如果任何关系通过把s改变为t在任何讨论下都没有改变。例如,在带有一个关系∈的集合论中,我们可以定义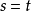 为
为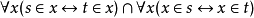 的缩写。这个等式定义接着自动的满足了关于等式的公理。
的缩写。这个等式定义接着自动的满足了关于等式的公理。
4.在某些理论中有可能给出特别的等式定义。例如,在带有一个关系 ≤的偏序的理论中,我们可以定义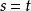 为
为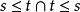 的缩写。
的缩写。
下面列出了一些重要的元逻辑定理。
1.不像命题演算,一阶逻辑是不可判定性的。对于任意的公式P,可以证实没有判定过程,判定P是否有效,(参见停机问题)。(结论独立的来自于邱奇和图灵。)
2. 有效性的判定问题是半可判定的。按哥德尔完备性定理所展示的,对于任何有效的公式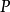 ,
,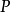 是可证明的。
是可证明的。
3. 一元断言逻辑(就是说,断言只有一个参数的断言逻辑)是可判定的2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国