在分析力学里,一个动力系统的拉格朗日函数,是描述整个物理系统的动力状态的函数,对于一般经典物理系统,通常定义为动能减去势能,以方程表示为
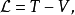 其中,
其中,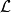 为拉格朗日量,
为拉格朗日量,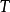 为动能,
为动能,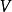 为势能。
为势能。
在分析力学里,假设已知一个系统的拉格朗日函数,则可以将拉格朗日量直接代入拉格朗日方程,稍加运算,即可求得此系统的运动方程。
概念拉格朗日量是动能 与势能
与势能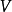 的差值:
的差值:
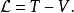 通常,动能的参数为广义速度
通常,动能的参数为广义速度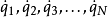 (符号上方的点号表示对于时间
(符号上方的点号表示对于时间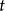 的全导数),而势能的参数为广义坐标
的全导数),而势能的参数为广义坐标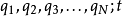 ,所以,拉格朗日函数的参数为
,所以,拉格朗日函数的参数为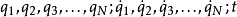 。解析一个问题,最先要选择一个合适的广义坐标。然后,计算出其拉格朗日函数。假定这些参数(广义坐标、广义速度)都互相独立,就可以用拉格朗日方程来求得系统的运动方程。
。解析一个问题,最先要选择一个合适的广义坐标。然后,计算出其拉格朗日函数。假定这些参数(广义坐标、广义速度)都互相独立,就可以用拉格朗日方程来求得系统的运动方程。
假设一个物理系统的拉格朗日量为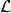 ,则此物理系统的运动,以拉格朗日方程表示为
,则此物理系统的运动,以拉格朗日方程表示为
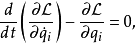 其中,
其中,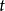 是时间,
是时间,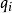 是广义坐标,
是广义坐标,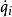 是广义速度1。
是广义速度1。
一个物理系统的作用量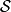 是一种泛函,以数学方程定义为
是一种泛函,以数学方程定义为
 其中,
其中,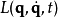 是系统的拉格朗日量,广义坐标
是系统的拉格朗日量,广义坐标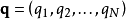 是时间
是时间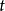 的函数,
的函数,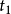 和
和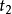 分别为初始时间和终结时间。
分别为初始时间和终结时间。
假若,作用量的一次变分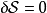 ,作用量
,作用量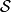 为平稳值,则
为平稳值,则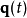 正确地描述这物理系统的真实演化。从这变分运算,可以推导出拉格朗日方程2。
正确地描述这物理系统的真实演化。从这变分运算,可以推导出拉格朗日方程2。
思考拉格朗日函数对于时间的全导数:
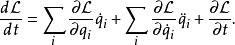 将拉格朗日方程代入,可以得到
将拉格朗日方程代入,可以得到
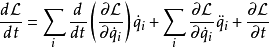
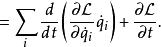
定义能量函数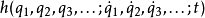 为
为
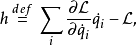 则能量函数与拉格朗日函数有以下含时关系式:
则能量函数与拉格朗日函数有以下含时关系式:
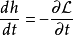
假若拉格朗日量显性地与时间无关,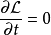 ,则能量函数是个常数:
,则能量函数是个常数: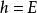 。称这常数
。称这常数 为这物理系统的能量。因此,这物理系统的能量守恒。
为这物理系统的能量。因此,这物理系统的能量守恒。
在分析力学里,一个动力系统的拉格朗日量(英语:Lagrangian),又称为拉格朗日函数,是描述整个物理系统的动力状态的函数,对於一般经典物理系统,通常定义为动能减去势能。
2.在力学方面在力学系上只有保守力的作用,则力学系及其运动条件就完全可以用拉格朗日函数表示出来。这里说的运动条件是指系统所受的主动力和约束。因此,给定了拉氏函数的明显形式就等于给出了一个确定的力学系。拉氏函数是力学系的特性函数。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国