[科普中国]-停泊轨道

简介

停泊轨道按中心体不同分为地球停泊轨道、月球停泊轨道和行星停泊轨道。地球停泊轨道是发射月球探测器、登月载人飞船、空间探测器和离地球较远的人造地球卫星（如静止卫星）的一个阶段，用于选择进入过渡轨道的入轨点，以弥补地面发射场地理位置固定的缺点，满足过渡轨道的要求。月球和行星停泊轨道用于选择进入轨道的起点，以保证航天器降落在天体表面的指定地区。对于返回地球的航天器，同样可以选择返回轨道的起点，以保证航天器能够准确进入再入走廊。此外，安排停泊轨道还为飞往新轨道之前提供最后全面检查航天器各系统可靠性的机会。1

设计优化近年来空间技术迅速发展，对空间目标的交会拦截技术成为各同研究的热点问题。空间交会(拦截)平台是一类能同时释放多个子飞行器实现对空间目标的交会、监测或打击、拦截任务的特殊类型航天器。由于面向多个目标，该类航天器停泊轨道参数以及子飞行器变轨时机的选择需要综合考虑多方面因素，进行多次折中权衡。空间交会(拦截)平台轨道运行示意图如图所示，平常整个平台在停泊轨道飞行，一旦接到任务指令即同时释放多个子飞行器，子飞行器在自身动力系统的作用下，通过轨道转移，实现对空间目标的交会或拦截任务。对目标的交会或拦截能力是该类平台的关键性能指标。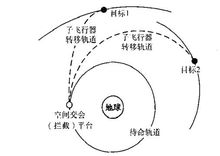

为了获得尽可能多的目标交会(拦截)机会，空间平台停泊轨道设计应以对目标的有效交会(拦截)区的最大化为优化目标，同时需要满足多目标交会(拦截)的要求。另外，成功交会(拦截)所采用的策略还应满足如下基本要求：1)轨道转移过程所消耗的燃料不能超过子飞行器可提供变轨速度增量要求；2)转移轨道不能与地面相交，其最低高度不小于100km；3)满足快速性要求，变轨飞行时间不超过上限。这些是是在有效交会(拦截)区确定过程中必须考虑的约束。这样，空间平台停泊设计优化模型除了停泊轨道要素外，还包括子飞行器变轨时间t。

常见优化算法包括全局优化算法和局部优化算法。由于停泊轨道参数设计问题设计域呈现复杂非线性和非连续性，寻优算法选用多岛遗传算法(MGA)这种探索式全局优化算法。它是一种在传统遗传算法基础上发展起来的一种“伪并行”优化算法，与传统遗传算法相比，使用精英保留和周期性迁移策略，更能保持解的多样性和全局性，有效抑制早熟现象的发生。2

轨道研究随着空间军事应用逐步从信息保障向空间作战的拓展，轨道机动作战成为一种新的作战模式。轨道拦截作为轨道机动的典型作战模式就是对己方的拦截器施加冲量， 使其变轨打击敌方的空间目标航天器，从而达到作战目的。在轨拦截器变轨前运行在停泊轨道( 驻留轨道) ， 停泊轨道的变化使得在轨拦截器有效拦截区域的变化， 导致覆盖控制的空间目标航天器不同。停泊轨道的优化使在轨拦截器覆盖尽量多的空间目标，可提高对敌威慑能力，具有一定的研究价值。

首先假设: (1) 地球为均匀球体，半径Rc=6371km；(2) 仅考虑地球引力， 忽略其他摄动力的影响；(3) 脉冲施加过程瞬间完成， 忽略脉冲施加过程中在轨拦截器位置的变化；(4) 在轨拦截器提供的脉冲幅值较小，可提供不超过 Δvmax任意方向的脉冲。

在轨拦截器停泊轨道优化过程为通过对轨道根数的迭代搜索， 使研究的指标达到最优。假定覆盖的空间目标航天器集合为 S' = { s1，s2，…，sK'} ( K'为覆盖的目标数) ，在此基础上通过对停泊轨道再调整， 使在轨拦截器拦截所有覆盖目标所需的总能量最小。能量越小则在轨拦截器的轨道保持能力越强， 更长时间保持在停泊轨道。

基于 OPSO 的在轨拦截器停泊轨道优化步骤为：

(1) 利用空间目标航天器信息确定在轨拦截器轨道根数的大致变化范围；

(2) 根据在轨拦截器轨道根数的大致变化范围及种群粒子个数， 选择相应的正交表产生初始化微粒群，对每个微粒产生一个初始速度， 并计算其适应度；

(3) 满足终止条件即结束迭代， 否则转入步骤(4)；

(4) 计算粒子自身最优解 pbi和种群最优解 pg；

(5) 以种群最优解为中心进行正交搜索， 计算适应度，选出其中最优解替代 pg；

(6) 更新粒子的速度和位置，返回步骤(3)。3

月球停泊轨道月球探测器的发射窗口是指能够满足轨道的运动学约束、光照约束和测控约束等条件的时间段，使探测器能够在一定的约束条件下与月球相遇，它又可分为月窗口和日窗口。

我国“嫦娥”工程的地月转移轨道则是基于大椭圆停泊轨道的近地点加速获得，其运动学约束特性呈现新的特点，运载运行可调的弧段很窄，转移轨道的近地点幅角和升交点赤经基本上是由运载分离后的轨道决定，所以对地月转移轨道设计增加了很强的制约。发射月球探测器实际上是使探测器与月球交会，由于月球位置的变化，不同的交会日期所对应转移轨道是不同的。

对于大椭圆停泊轨道，从节省能量的角度出发，探测器一般在近地点沿速度方向加速进入转移轨道，保证转移轨道与停泊自轨道共面，所以停泊轨道决定了转移轨道的升交点赤经和近地点幅角。这种情况下停泊轨道的近地点、探测器从地面发射进入停泊轨道的入轨点和转移轨道的入轨点在惯性空间三点合一，本文重点分析地月转移轨道段。因此可以分析不同时刻对应的探测器地月转移轨道入轨点分布规律。

在一个恒星月内探测器人轨点纬度为0°和地月转移轨道的近地点幅角为180°(满足我国长三甲运载要求)的情况只有两次，说明我国长三甲运载在一个月内有两次发射机会。另外，对我国的这两次发射机会来讲，交会时月球的赤纬均为0°，也即是月球均处在白道相对于地球赤道的升交点和降交点附近，这充分体现了我国大椭圆停泊轨道地月转移轨道发射窗口基于运动学约束的内在规律。我国在进行大椭圆停泊轨道探测器发射窗口设计时可以利用这一特点获取探测器入轨时刻的初值。

大椭圆停泊轨道下地月转移轨道的发射窗口是零窗口，但可以通过调整转移初速增加发射窗口，使探测器在连续几天有入轨机会。4