[科普中国]-大圆航线

球面上两点之间的最短距离的航线就是大圆航线。大圆航线是远距离航行的飞机规划航路时经常采用的航线。地球是一个椭球体，托球面上的问题解算十分复杂，因此，在实际应用中，往往把地球看做一个正球体。地球面上两点间最短距离是通过两点间大圆的劣弧。大圆航线的计算 包括初始航向角、航程、各分点坐标的计算。2大圆航线距离最短，但导航较困难。因此实用中通常采用长距离靠近大圆航线，而短距离走等角航线的作法。

地球是一个椭球体，由于椭球扁率的影响，椭球面上的大地问题解算十分复杂。在实际应用中，往往把地球近似看作是一个正球体，这样，利用球面三角形的相关公式，大圆航线的解算就可以大大地被简化。

在球面上由三个大圆弧相交于三点所围成的球面部分称为球面三角形，构成三角形的大圆弧称为球面三角形的边，由两个大圆弧相交而成的球面角称为球面三角形的角。AB、AC、BC所围成的三角形便是一个球面三角形，通常用A、B、C表示球面三角形的三个角；用a、b、c表示球面三角形的三条边(图2-16)。这三个角A、B、C和三条边a、b、c合称为球面三角形六要素。由于a、b、c都是大圆弧，所以也都可以用弧度表示。3

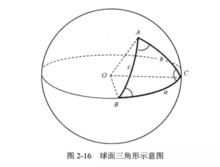
这里，先介绍三组球面任一三角形的基本公式：

（1）球面正弦公式(2-6)：

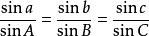
（2）边的余弦公式(2-7)：

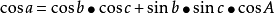
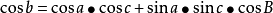
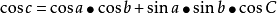
（3）球面三角形余切公式（2-8 四联公式）：

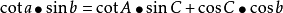
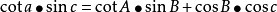
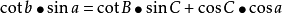
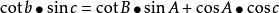
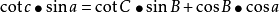
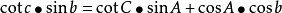
这些公式表明了各要素之间的相互计算恭喜，是后面工作的基础。根据图2-17，进行解算P1、P2的大圆航线。

P1、P2为地球上的两点，N是北极点。那么P1、P2，N就构成了一个球面三角形。首先要确定这个三角形的六要素中，哪些是已知的，哪些是要求解的。P1的经纬度已知，P1N为（90°－B1），同理，P2的经纬度已知，P2N为（90°－B2），角N为P1、P2之间的经纬度差（L2－L1），这些都是已知的。通过前面列出的公式，不难推出大圆航线距离公式和大圆航线正方位角公式。3

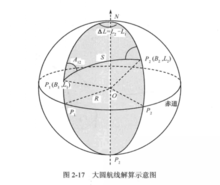
大圆航线距离公式为（2-9）：

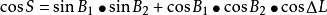
大圆航线正方位角公式（2-10）：

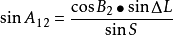
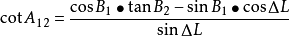
用公式计算，S是弧长，单位是弧度（rad），只要乘以地球的平均半径，就可以得到距离了。初始方位角，用这两个公式中的任何一个，再用反正弦或反正切，就可以计算出来。但有问题，因为方位角定义为大圆航线与经线的夹角，取值范围为0°～360°。而反正弦或反余切的值域都是－90°到90°，不能直接得到0°～360°的航线角，也就是说，我们还必须判断航线角的象限，然后再进一步处理。这里得到两个计算航线角的解算公式，它们恰好可以相互约束，帮我们判断。

理论上，两点之间的大圆航线是一条空间曲线，由沿途无数个中间点组成，所以，在实践中，我们不可能去解算无数个点的坐标。实际上，我们都是用折线去近似代表这条曲线。所谓的解算，就是去计算有限个中间点的经纬度坐标。这里介绍一种称为弦线法的解算方法。

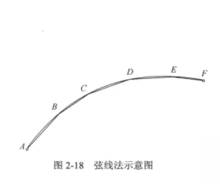
如图2-18所示为A、F之间的一条大圆航线，弦线法就是按照一定的经度间隔，计算出航线上相应的中间点B、C、D、E等各点的纬度，然后将这些点连接起来，形成的这条折线就是近似的大圆航线的轨迹。

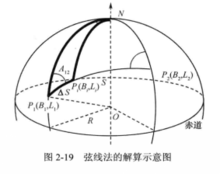
设Pi为第i个中间点，△S为解算的间隔距离（根据精度要求确定），则NP1Pi构成一个球面三角形，其中，已知条件有弧NP1、弧P1Pi（即△S）和∠NP1Pi（即A12），根据球面三角形的相关公式，即可解出弧NPi的值，由此可得到Pi的纬度（用90°减去弧NPi即可）。同时可以解算∠P1NPi，也就是P1和Pi的经差，进而解算出Pi的经度，由此，Pi的经纬度Pi（Bi，Li）就可以算出来了，就可以得到大圆航线P1P2之间一系列中间点的经纬度坐标，将这些点连接起来，就可以得到近似的大圆航线轨迹（2-19）。3