[科普中国]-轨道力学

人造天体与自然天体在万有引力场中的运动规律类似，因此轨道力学的很大一部分内容源自天文学中的天体力学，而天体力学的发展则可追溯到早期的古典天文学。

1、原始天文观测时期

生活在地球上的人类，很早以前就对一些基本的天文现象有了认识。先民们通过肉眼观测天体，将天象及其变化记录成册，以此来辨别方向、确定时辰、编制历法，安排重大的社会活动。大约在公元前4000年，古埃及人就注意到每当天狼星第一次于日出之前在东方的地平线上出现，尼罗河就开始泛滥，这个天象被称为天狼星的偕日升。古埃及人把偕日升作为一年的开始，经过长期观测确定出两次天狼星偕日升的时间间隔为365．25天，并以此为基础建立了历法，这就是现在全世界通行的公历的前身。我国天文学的起源可追溯到久远的年代，在最古老的历史文献《尚书 尧典》中就有记载：“寅宾日出，平秩东作，日中星鸟，以殷仲春”，是说当日出正东时就是春分日，要举行祭祀，以利农耕。在我国汉代已经出现了比较精确的日晷，通过测量日影的移动来确定时辰，如图1-l所示。1

古人观测天象除了作为一种实用的生存手段外，神秘的天象也给人在感性上带来惊异和敬畏的冲击，人们企图利用天上出现的偶然现象对人间事务和个人命运进行预测，这就是星占。在古巴比伦就有一批职业的星占学家，时刻关注和记录着天空的变化，长期以来形成了可观的天象记录与对应解释，图1-2是公元前17世纪古巴比伦记录金星动态的泥板文书。星占学家希望有能力把握太阳、月亮和行星的运动规律，从而能预测各天体在未来某个时刻的位置，以期借此预测人间的事务。记载有未来某时刻及对应时刻天体位置的表称为星历表。事实上，对星历表精益求精的追求，一直到17世纪都是研究天体运动规律背后的驱动力，当然目的不再仅局限于星占。

2、古希腊天文学

古希腊天文学对天体运动的描述和解释构成了古典天文学的主体。古希腊民族喜好辩论、崇尚理性、讲学之风盛行。从公元前6世纪的泰勒斯到公元2世纪的托勒密近800年间，古希腊天文学发展迅速，先后出现过四大学派。

爱奥尼亚学派由泰勒斯(Thales，约公元前624-546)创立，其主要贡献是把古巴比伦和古埃及的天文学知识介绍到希腊。该学派认为可见天空是完整球形天空的一半，圆盘状的大地倒扣在球体中心，星辰都随同天空围绕北极星旋转。1

毕达哥拉斯学派由著名几何学家毕达哥拉斯(Pythagoras，约公元前570-496)创立，该学派对数最感兴趣，特别强调脱离形式的纯粹的数，因此容易导出这样一种观点，即行星在天空中复杂的视运动可以看成多种简单运动的复合结果。该学派的菲洛劳斯(Philolaus，约公元前480-385)提出了一个地动学说，认为地球、太阳、月亮和行星都围绕着一团中央火运行，太阳是一面大镜子，反射了中央火发出的光芒，日月五大行星的视运动是地球也在运动的反映。毕达哥拉斯还根据月食时阴影的边缘是弧状的，推测出地球是球形的。

柏拉图学派由哲学家柏拉图(Plato，约公元前427-347)创立，该学派接受毕达哥拉斯学派圆是最完美图形的观点，并用这个观点解释宇宙。柏拉图试图使天文学成为数学的一个分支，并提出了一个后面几个世纪的天文学家都致力于解决的首要问题：能否用匀速而整齐的运动解释行星的视运动。因为相比于太阳、月亮和恒星的运动，解释五大行星不规则的视运动是最复杂的题（图1-3)。柏拉图的学生欧多克斯(约公元前410-356)提出了同心球理论，试图 解决柏拉图所述的天文课题。欧多克斯设想地球是宇宙的中心，每一个天体复杂的视运动轨迹 都是由若干个同心球的匀速圆周运动复合而成的，为此毎颗行行星要设置4个同心球。亚里士 多德(Arisimle，公元前384-322)作为古希腊最伟大的思想家，在天文学方面支持欧多克斯的同 心球理论。他坚持认为大地是不动的，否则一定会观测到恒星的周年视差。在以后的两千多年 间，这个理由一直是地球不动的重要证据，因为宇宙的广袤远远超出了古人的想象空间。亚里士 多徳还提出了自己的运动学与动力学理论，认为物体在不受外部影响的情况下将处于静止状态, 因此解释物体的运动必须寻找外部的原因，这为地静说反对地动说提供了理论依据。1

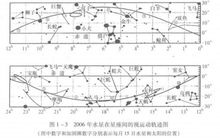
亚历山大学派形成于亚历山大大帝远征时期，它将古希腊的几何天文学与古巴比伦的算术天文学高度融合，开启了古希腊天文学新的历史时期，又称希腊化时期。这一时期的天文学人才济济，成果累累。阿里斯塔克(Aristarchus，公元前310-230)在一篇名为《论日月的大小和距离》的论文中，基于希腊几何学的演绎推理，得到太阳是一个比地球直径大6～7倍的球体的结论(图1-4)，鉴于大的物体绕小的物体转动不合常理，因此阿里斯塔克认为地球和五个行星都以太阳为中心运转。由于地球每年绕日一周，同时每天白转一圈，所以才产生天体的周年变化和周日视运动，、他还认为由于恒星离地球的距离太过遥远，因此地球公转导致的恒星周年视差很难观测到。阿里斯塔克是第一个提出严格的日心地动观点的学者，被称为哥白尼的先驱。

以一部《圆锥曲线论》闻名数学史的阿波罗尼乌斯(Apollonius，公元前262-190)在用匀速圆周运动描述天体运行时提出了两种方案。在第一个方案中，行星绕地球运动，但地球并不处于圆周的中心，而是偏向一边，行星在偏心圆上作匀速运动。第二个方案中，行星在一个较小的圆周“本轮”上作匀速运动，而本轮的中心则在一个较大的圆周“均轮”上作匀速运动，地球位于均轮的中心(图1-5)。阿波罗尼乌斯的这两个数学发明为天文学家解决行星视运动问题提供了基础。喜帕恰斯(Hipparchus，旧译依巴谷，公元前190-127)利用阿波罗尼乌斯的偏心圆模型来描述太阳的运动，很好地解决了四季长度不等与匀速圆周运动的矛盾。喜帕恰斯还是一位勤奋的观测者，他对恒星方位进行了精密的测量，编制了包含有1080个恒星的星表，对促进西方天文学的发展起了很大作用。通过比较自己与前人的观测数据，喜帕恰斯还发现了春分点的退行即岁差现象。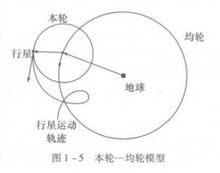

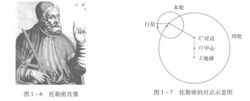
在喜帕恰斯之后的300年中，古希腊天文学进展不大。最令人瞩目的工作是古埃及天文学家托勒密(Ptolemy，约公元后100-170，图1-6)完成的，他集古希腊天文学之大成，写成巨著《至大论》(后来被阿拉伯人译为《天文学大成》)。托勒密继承了偏心圆、本轮和均轮的假设，又引人了一个重要的概念——“对点”。对点是地球在偏心圆中相对于圆心的镜像，圆周上的点不是作匀速运动，而是变速运动，速度变化的规律是让对点上的观测者看起来是匀速的(图1-7)。基于托勒密提供的宇宙几何模型，能对13月和五大行星的运动给出相当精确的预报，而且从数学上讲，当一级本轮预报精度不足时，还可以增加次级，乃至三级、四级本轮，直到获得足够的预报精度。但增加本轮的同时也增大了数学计算的难度，有文献讲哥白尼看到的托勒密体系有多达80个本轮，数学计算极其繁复，以致要从简单性出发进行改革。此外，对点的引入使得天体的运动不再是匀速运动，这在许多人看来是对古希腊原则的冒犯，因此也成为改革托勒密体系的原因之一。无论如何，托勒密的工作代表了人类对认识自然的理性追求，是那个时期人类智慧的最高代表。在此之后的一千多年内，《至大论》一直被欧洲和西亚人奉为经典。1

3、阿拉伯天文学

托勒密写成《至大论》之时，雅典文化已趋势微。从公元476年西罗马帝国衰亡至公元15世纪文艺复兴的1000年间，欧洲的天文学几乎没有进展。这段时期，世界范围内天文学的进步主要在阿拉伯世界。

阿拉伯人通过对周边先进文化的大翻译运动，激励了自身天文学的起步与发展。他们很重要的一项贡献是发展了球面三角学，极大地提高了天文学的计算能力。巴格达学派的阿尔巴塔尼第一个在天文计算中引入了正弦函数，发现了球面三角形的余弦定理，完善了球面三角的计算方法。他还首次对托勒密的计算进行了改进，纠正了太阳的远地点进动值和岁差常数，改进了回归年的长度。他最重要的一部著作是57卷的《历算书》，哥白尼、第谷、开普勒等人都受到过该书的影响。1

阿拉伯人在天文观测方面也做出了很大贡献。他们制作了大量的大型精密观测仪器，还发明了特有的仪器星盘，提高了天文观测精度，出版了《托莱多天文表》、《乌鲁伯格星表》等著作，后者被认为是介于托勒密和第谷之间最重要的恒星星表。针对托勒密模型中偏心圆和对点的不完美性，阿拉伯的学者们也提出了一些替代模型。马拉盖天文台的图西(AI-Tusi，1201-1284)只是用匀速圆周运动就完成了行星运动模型的构建，代价是每个行星运动模型增加两个本轮。图西还构想过一种椭圆轨道的可能模型。同样是马拉盖学派的学者沙提尔(A1-Shatir，1304-1375)，他发展了图西的双本轮模型，通过巧妙的设计消除了托勒密的对点和偏心圆，并在模型精度上首次超越了托勒密的模型。沙提尔非常重视测量精度和对理论进行实测检验，他是第一位为检验托勒密模型而把实验引入行星理论的天文学家。1

12世纪以后，大量的阿拉伯人著作被译成拉丁文，希腊人的学说以这种迂回的方式重新进入拉丁世界，推动了现代天文学的诞生。比如，哥白尼的日心理论中消除托勒密对点和偏心圆的方法与沙提尔的模型在数学细节上几乎一致，两者的月亮运动模型也是一样的，因此人们有理由相信沙提尔的模型被哥白尼改编进了他的理论之中。

天体力学(Celestial Mechanics)是应用数学和力学理论研究天体的运动和形状的学科，它是近代自然科学发展的先锋，直接促进了经典数学和力学理论的诞生与发展。天体力学的起源始自牛顿的经典著作《自然哲学的数学原理》，但正如牛顿所说，该书的形成是“站在巨人的肩上”，几位先驱者的工作为牛顿的成就奠定了基础，而人类历史上最伟大的数学家们的参与则使得天体力学的发展终臻大成。1

天体力学的发展始自15世纪欧洲文艺复兴时期，这一阶段资本主义开始兴起，为了追逐利润需要对外扩张，海上交通迅速发展。航海事业对精密星历表提出更高的要求，从而引起天文学的大发展。天体力学的发展总体上可以分为三个阶段，即萌芽期、奠基期和发展期。

1、萌芽期

这一时期学者们的主要工作是从天体观测数据中探寻天体的运动规律，并尝试解释天体运动的原因，做出杰出贡献的科学家主要有哥白尼、第谷、开普勒、伽利略、笛卡儿等人。1

2、奠基期

这一阶段自17世纪牛顿创立天体力学到19世纪后期，是天体力学的奠基过程。天体力学在这个过程中逐步形成了自己的学科体系，称为经典天体力学。它的研究对象主要是太阳系内的大行星和月球，研究方法主要是经典数学分析方法，即摄动理论。1

3、发展期

自19世纪后期到20世纪50年代，是天体力学的发展期。在研究对象方面，增加了太阳系内大量的小天体，如小行星、彗星和行星卫星等；在研究方法方面，除继续改进分析方法外，增加了定性方法和数值方法，但它们主要作为分析方法的补充。这段时期可以称为近代天体力学时期。1

轨道力学是航天动力学的重要组成部分。航天动力学(Astrodynamics)是应用数学、力学和控制理沦研究航天飞行器运动规律和控制方法的科学，它是随着火箭推进技术和控制理论的发展而逐渐兴起的。航天动力学的主要研究内容可分为三个方面：

火箭动力学：研究推进装置工作时飞行器质心的运动与控制规律；

轨道动力学：研究在中心天体引力和其它摄动力作用下质心的运动规律；

姿态动力学：研究飞行器相对于自身质心以及各组成部分问的姿态运动与控制规律。

航天器的轨道包括发射轨道、运行轨道和返回轨道，因此轨道力学的研究内容既包括轨道动力学，又包括火箭动力学。虽然轨道力学也采用天体力学的研究方法，但它已经超出了传统天体力学的研究范围。一方面，绝大多数航天器运行在近地空间，受力环境复杂、轨道角速度大，因此摄动分析与精确轨道计算更加困难；另一方面，由于能够根据需要设计和改变航天器的飞行轨道，轨道设计、轨道控制成为重要的研究内容。

与天体力学不同，航天动力学的发展大多是由大型航天工程推动的，研究内容更加注重实用性。以1957年发射第一颗人造地球卫星为界，航天动力学的发展大致可以分为两个阶段。1

1、早期发展

航天动力学的早期发展阶段主要是对火箭推进技术的探索。

俄国科学家齐奥尔科夫斯基(Konstantin Tsiolkovsky，1857-1935，图1-21)是现代航天学和火箭理论的奠基人。1898年，他完成了著名论文《用于空间研究的反作用飞行器》，推导了理想情况下计算火箭速度增量的齐奥尔科夫斯基公式，并建议使用液氢/液氧的液体推进剂和多级火箭。苏联的另一位太空飞行先驱灿德尔(Friedirch Tsander，1887-1933)积极宣传和推动齐奥尔科夫斯基的研究工作，并于1931年在莫斯科组建了“反作用推进研究小组”(GIRD)，刚从大学毕业的科罗廖夫(Sergey Korolyov，1907—1966)参加了小组的筹建。1933年，GIRD研制的火箭发射成功，飞行到了75m左右的高度，这是苏联发射成功的第一支火箭。这时GIRD已经与另一个火箭研究小组合并组成新的研究机构“反作用推进科学研究所”，科罗廖夫被任命为副主任，并逐渐成长为冷战期间苏联火箭设计的灵魂人物。1

美国科学家戈达德(Robert Goddard，1882-1945)是火箭理论与技术的先驱。1919年，戈达德在史密森学会发表了名为《一种达到极大高度的方法》的论文，详细叙述了火箭飞行的数学理论，并论证了空间飞行与飞向月球的可能性。戈达德更大的贡献是在火箭试验方面(图1-22)，他于1926年成功试射了世界上第一枚用液体化学燃料作动力的火箭，并设计了多级火箭，每级火箭都将载荷推到更高的高度，直至飞出大气层，这种设计思想一直沿用到今天。戈达德还成功试射了第一枚用电力控制的火箭和用陀螺仪控制的火箭，第一个将拉瓦尔喷管和涡轮一泵系统应用到火箭发动机上。德国科学家利用他的设计思想制造了V-2火箭(图1-23)。戈达德一生获得了214个火箭方面的专利，其中大多是关于液体燃料火箭和相关部件的。为纪念他，1959年美国航空航天局(NASA)以他的名字命名了一个新成立的飞行控制中心。1

德国火箭专家奥伯特(Hermann Oberth，1894-1989)奠定了液体火箭的理论基础，被誉为欧洲火箭之父。奥伯特的主要贡献是理论上的，他在1923年发表了经典著作《飞往星际空间的火箭》，为早期火箭技术的发展奠定了理论基础。1929年，奥伯特成立了一个火箭制造小组，柏林工大的学生冯·布劳恩(WernheJ von Braun，1912-1977)参与了这个小组。后来，奥伯特和冯·布劳恩参加了纳粹德国的火箭计划，冯·布劳恩被任命为技术总负责人，研制出了以乙醇/液氧为推进剂的V-2火箭。V-2火箭的射程达320km，最大速度6Ma，使用的A-4火箭发动机完全是以奥伯特的理论框架为基础的。第二次世界大战结束后，冯·布劳恩被招募到美国，成为冷战期间美国火箭设计的领军人物。为完成“阿波罗”登月计划，在冯·布劳恩的领导下美国研制成功了巨型运载火箭“土星V号”，起飞推力达3400t，达到了当时火箭技术的最高成就。1

2、近期发展

航天动力学的近期发展是以一系列的航天工程为背景，在解决实际的工程应用问题中逐渐进步的。

1957年10月4日，苏联的第一颗人造地球卫星Sputnik发射升空，开启了人类探索太空的序幕(图1-24)。一个月后，苏联发射了第二颗卫星SputnikⅡ，并搭载了一条名为“莱依卡”的小狗，同时实现了对太阳紫外线、x射线和宇宙射线的探测。1958年1月，美国的第一颗卫星“探索者”1号成功进入地球轨道。1960年，美国发射了“回声”I号，它带有铝制外壳，可以被动地反射声音和图像信号，向人们展示了卫星通信的可行性，人类开始利用太空来改善自己的生活。1964年，美国发射了第一颗实用的地球同步卫星，并借助这颗卫星转播了东京夏季奥运会。此后，各类科学卫星、通信卫星、气象卫星、遥感卫星、导航卫星陆续发射升空，目前已有6000多颗，全方位地改变了人类的生活。离开地球进入太空一直是人类的梦想。1961年4月12日，苏联航天员尤里·加加林乘坐“东方”1号宇宙飞船进入太空，绕地球飞行一周后安全返回地面，实现了人类的第一次太空飞行。1966年1月，两艘“联盟”号飞船在轨道上完成交会对接。1971年，苏联第一个空间站“礼炮”l号发射升空，并与“联盟”号飞船对接成功。1981年4月，美国航天飞机“哥伦比亚”号进入太空，绕地球飞行36圈后成功返回地球并实现水平着陆。1996年，经过10年的建设周期，第一个真正意义上的空间站“和平”号完成建设，但在4年后就因部件老化和缺乏维修经费而坠入地球大气烧毁。我国经过40多年的努力，已发射了百余颗人造地球卫星，完成了载人航天、交会对接等重大任务，目前正在实施空间站建设。数量众多的近地航天器的发射和运行，带来了轨道摄动分析、轨道设计、轨道机动、相对运动控制等一系列崭新的课题，为轨道力学的发展提供了广阔的空间。1

了解宇宙的起源与演变，探究生命存在的意义一直是人类最感兴趣的话题。早期人们只能借助天文望远镜观测地外天体，太空飞行技术提供了新的研究手段。月球作为地球唯一的天然卫星，也是离地球最近的天体，自然成为深空探测的第一个目标。1959年1月2日，苏联的“月球”1号顺利升空，并未经停泊直接奔向月球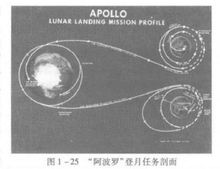，成为第一个达到第二宇宙速度的人造物体。可惜的是，由于计算错误，“月球”1号未能实现预期的撞月目标。同年9月，“月球”2号成功撞击月球；10月，“月球”3号成功绕到月球背面，传回了第一张月球背面的图片。1966年1月，“月球”9号成功实现月面软着陆。1970年9月，“月球”16号到达月球后采集月壤样品101g，并成功返回地球。美国最成功的月球探测项目当属“阿波罗”计划。1961年，美国启动“阿波罗”计划。作为前期准备，先后发射了三个系列的月球探测器，即“徘徊者”(Ranger)、“勘察者”(Surveyor)和“月球轨道器”(Lunar Orbiter)，为了解月貌、选择登月着陆点完成了技术准备。1969年7月，“阿波罗”11号实现月球软着陆，阿姆斯特朗在月球上留下了人类的第一个脚印(图1-25)。我国在2004年发射了第一颗月球探测器“嫦娥”一号，实现了对月球的环绕探测。2013年，“嫦娥”三号探测器成功实现月面软着陆。1

行星和行星际探测器加深了人类对太阳系的认识。1960年3月，美国成功发射了第一个行星际探测器“先驱者”5号，进入了一条椭圆日心轨道，测量了行星际磁场、行星际粒子和太阳风。金星和火星是目前人类探测最多的两颗除地球之外的行星。1962年，美国的“水手”2号成功飞掠金星，发现金星没有磁场和辐射带。1970年，苏联的“金星”7号第一次降落金星表面。1964年，美国发射的“水手”4号成为第一个飞掠火星的探测器，首次传回了另一颗行星的图像，并测量了火星的大气和辐射情况。1975年，“海盗”1号在火星表面软着陆成功，发回了几万张火星表面的照片。除了探测大行星外，人类也向小行星、彗星以及太阳发射了多个探测器，如“近地小行星会合”探测器(NEAR)、“星辰”号(Stardust)彗星探测器、“尤利西斯”号(Ulysses)太阳探测器等。1977年发射的“旅行者”1号尤其值得关注。发射入轨后，“旅行者”l号先后探测了木星、土星和土星最大的卫星“泰坦”。2013年9月，NASA宣布“旅行者”l号已经离开太阳系，进入星际空间，成为目前飞得最远的人造物体(图1-26)。与近地航天器相比，深空探测器在轨道设计和控制方面有更多的新技术可以利用，因此设计的空间也更大。比如，1978年发射的“国际日地探测器”3号(ISEE-3)入轨到日地L1平动点的晕轨道(Halo orbit)，实现对日地关系、太阳风和宇宙射线的探测，是第一个平动点探测器。1990年，美国和欧空局发射“尤利西斯”号太阳探测器，借助于木星强大的引力实施变轨，最终使探测器离了于黄道面进入环绕太阳的极地轨道。1998年，美国发射“深空”实验航天器Deep Space-1，验证了以电推进作为主推进的可行性，小行星探测器“黎明”号(DAWN)、月球探测器SMART-1等也都以电推进作为主推进器实现了预期任务。在长期的轨道转移过程中，电推进可能比传统的化学推进更节省燃料，但轨道设计的难度也更大。2001年，美国发射了“起源”号(Genesis)探测器用于收集太阳风样品，这是第一个采用现代动力系统理论设计轨道的航天器。平动点、近旁转向、电推进、动力系统理论等新技术，以及大行星、卫星、小天体、日地空间等众多的探测对象给深空探测轨道设计提供了广阔的空间，成为目前轨道力学领域研究的热点。1

轨道动力学研究航天器质心在外力作用下的运动规律，基本的描述公式是牛顿第二定律：(1-2-1)

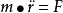（1-2-1）

式中，为航天器相对于惯性系的位置矢量；F为作用在航天器上外力的主矢。

1、N体问题

若有N个天体，各天体的质量分布是球对称的，则在考虑彼此间的引力作用时，可以认为是质量集中在球心的质点。若N个天体除了相互间的引力作用外，不受其它外力的作用，则称为N体系统。已知N体系统中各质点在t0时刻的位置和速度，求此后任意时刻t的位置和速度的问题，称为N体问题。

N体问题是天体力学的经典问题，也是最基本的问题。从牛顿开始，许多数学家和天文学家都研究过这个问题，但只在个别情况下求得了解析解。今天，人们仍在不断尝试用各种先进的数学手段探求N体问题的解。

N=2时称为二体问题。二体问题有解析解，它的几何形状是一条圆锥曲线，可以用六个常值的轨道要素来描述。二体问题是描述航天器在天体引力场中运动时最常用的理想化模型，是轨道力学的核心内容。

2、轨道摄动

精确的理论轨道与简化的理论轨道之差，称为轨道摄动。此时，可把式(1-2-1)写成(1-2-2)

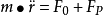（1-2-2）

式中：F0为把中心天体看作匀质圆球时的万有引力，是航天器上的主要作用力；Fp为其它作用力，包括中心天体的非球形引力、其它天体的引力、大气阻力、太阳辐射压力等，称为摄动力，一般有Fp远小于F0。

不考虑Fp时，求解式(1-2-2)得到的即是简化的理论轨道，即二体轨道。考虑Fp时求解式(1-2-2)得到精确的理论轨道，此时轨道要素成为随时间变化的量。研究轨道要素在摄动力作用下的变化规律是轨道摄动的主要研究内容，也是经典天体力学的主要研究内容。

计算轨道摄动的主要目的是求出航天器精确的轨道运动，获得其在任何时刻准确的位置与速度。还可以通过与实测轨道的对比，研究分析轨道摄动的变化，为天体引力场、大气密度、地震预报等研究服务。

3、轨道确定

根据轨道测量数据确定航天器真实运行轨道的过程称为轨道确定，简称定轨。航天器入轨时由于发射误差的影响，实际轨道会与标称轨道存在偏差；在轨运行一段时间后，由于摄动力的影响，实际轨道也会偏离标称轨道。为完成预定任务，必须通过测量手段确定航天器的实际轨道。

轨道测量往往无法直接获得航天器的位置、速度矢量或轨道要素，而是要通过转换得到。不同的测轨数据有不同的换算方法。如光学望远镜一次测量能获得两个角度数据(赤经和赤纬），得不到距离信息，至少要经过三次测量才能得到轨道要素。若采用雷达测轨，一次测量可以获得相对距离和两个角度信息(方位角和仰角)，结合雷达的地面坐标可以得到卫星的地心位置，经过两次测量可以计算轨道要素。定轨初期，根据少量的测量数据粗略确定航天器轨道的过程称为初轨确定。由于测量数据中含有各种误差，因此初轨确定的精度一般不高。为提高精度，往往要利用大量的测轨数据和摄动运动模型，根据现代估计理论滤除随机测量误差，该过程称为轨道改进。

轨道确定是现代航天应用巾不可或缺的技术手段，早期对它的研究则有力地推动了天体力学的发展。

4、轨道设计

航天器的发射和在轨运行并不是独立的，要与地球、太阳等天体发生信息联系，以完成预定的任务。例如，为完成对地勘察、通信、测量等任务，要分析航天器的星下点轨迹和星上有效载荷对地面的覆盖区域；为制定热控系统、电源系统、姿控系统的工作模式，要分析与太阳的几何方位；为完成定姿、定轨等任务，要确定与恒星的相对方位关系；为与其它航天器协同完成某些任务，要分析相互间的相对位置关系。在月球探测、行星际航行等任务中，多以接近目标天体为目的，实现这个目的的可能轨道有很多条，要从中选出一条最佳轨道，使航天器能够以最小的燃料消耗或最短的飞行时间、用最简单的飞行控制方法、在最便于测控的情况下到达天体附近。

上述要求给航天器轨道设计提出了多种约束条件，在这些条件下确定航天器的飞行轨道，并使某些性能指标达到最优是轨道设计的主要研究内容。

轨道控制又称轨道机动，主要研究如何改变作用在航天器上控制力的变化规律，使航天器的质心运动轨迹满足预期要求，可以用公式表示为(1-2-3)

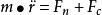（1-2-3）

式中：Fc为能够改变的控制力；Fn为其它作用力。

很明显，微分方程(1-2-3)的解与Fc(t)的变化规律有关，轨道控制的目的就是根据任务要求的r(t)设计Fc(t)的变化规律。

1、轨道改变与轨道转移

这种轨道控制方式是使航天器从一个自由飞行轨道转移到另一个自由飞行轨道，且转移过程中速度增量较大。若初轨道与终轨道相交，通过一次变轨即可完成轨道机动过程，则称为轨道改变；否则称为轨道转移。根据控制力特性的不同，又可以分为脉冲推力、有限推力、小推力等不同情形。这种轨道机动方式常用于地球同步轨道卫星发射、交会对接远程段控制、返回式卫星离轨段控制、月球或行星探测器发射等航天任务。发射地球同步卫星时，一般先将卫星送入近地停泊轨道，然后通过一次或多次轨道转移最终进入同步轨道。深空探测器在飞行过程中经常要经过多次变轨，由于飞行距离远、速度增量大、引力场变化复杂，可以采用近旁转向、气动辅助变轨、小推力推进等技术，转移轨道设计难度大。2

2、轨道调整

轨道调整的特点是初轨道与终轨道的轨道要素相差不大，轨道机动需要的速度增量较小，因此可以用轨道摄动运动方程或线性化的运动方程描述变轨过程。这种控制方式的典型应用包括航天器入轨后的初始轨道捕获、地球静止卫星的位置保持、对地观测卫星的位置支持、无阻力卫星的扰动补偿、星座或编队飞行时卫星的相对位置保持、深空探测轨道的中途修正等。地球静止卫星的位置保持是典型的轨道调整任务，目的是使卫星与地球的相对位置保持不变，这就要求轨道周期等于地球的自转周期，偏心率和轨道倾角都接近于零。深空探测器的飞行距离远，行星或行星际空间的探测至少要飞行几个月的时间，很小的初始误差都会被放大到不可接受的程度，因此在任务设计阶段要仔细进行误差分析，安排好若干次中途修正，保证到达目标天体。2

3、相对运动控制

相对运动控制是指两航天器的相对距离较近，具备相对导航的测量条件，可以用相对运动方程描述的轨道机动问题。这种控制方式的应用任务包括交会对接、编队飞行、轨道拦截的末段控制等。相对运动控制的研究主要集中在近地空间，近年来逐渐扩展到深空任务，特别是平动点编队、平动点交会等。交会对接是一种典型的相对运动控制任务，一般先通过远程导引段将追踪航天器导引到目标航天器附近(比如小于100km)，追踪器携带的雷达、差分GPS、光学敏感器等能够获得相对运动信息后，则开始近程导引。近程导引段一般基于线性化的相对运动方程(如C-W方程)设计控制律，对相对运动状态实施闭环控制，直至满足停靠或对接要求。轨道拦截末段控制也是一种典型的相对运动控制，它与轨道交会的区别在于不控制相对速度，只要求末端相对位置为零。轨道拦截一般通过雷达或光学导引头获取两个航天器的相对运动信息，基于视线坐标系内的相对运动方程设计控制律。2

航天器是一类有控飞行器，它与自然天体的一个重要区别是运行轨道可以人为选择，而且运行过程巾可以通过施加控制力加以改变。因此，根据特定的航天任务，选择最有利的运行轨道、制定最优的控制策略是航天任务中最重要的设计内容之一，轨道力学正是解决这一问题的。轨道力学在航天器任务分析、总体设计、分系统设计、发射与运营管理、应用效果评估等全寿命周期内的各个环节都有非常重要的应用，下面以太阳同步轨道气象卫星为例加以说明。2

为实现对既定区域气象特征的良好观测，气象卫星一般选择两类轨道，太阳同步轨道或地球静止轨道。我国的“风云”气象卫星以奇数编号的都是太阳同步轨道(图1-27)，以偶数编号的都是地球静止轨道。太阳同步轨道的特点是轨道面与太阳的夹角基本不变，卫星星下点经过相同纬度的当地地方平时是一样的，因此光照条件相同，便于卫星云图的判读。2

在卫星设计中，轨道特性对其它分系统设计至关重要，因此首先要根据卫星任务要求，初步确定卫星的轨道。太阳同步轨道的实现原理是地球扁率项引起的轨道面进动速率与平太阳周年视运动的角速率相同，因此轨道倾角、偏心率与轨道高度之间满足一定的约束条件。为保证云图质量，轨道一般选择为圆轨道，偏心率小于1‰。轨道倾角要大于90°，为实现全球观测，最好选择在极轨附近，由此可确定轨道高度在800～1000km。同时，希望气象卫星能够在一段时间内实现对特定地点的重复访问．即轨道要求是回归或准回归轨道。考虑上述因素，以及运载火箭、地面测控网、卫星寿命、有效载荷等约束条件，可以初步确定卫星的轨道参数。2

卫星轨道会影响有效载荷设计，轨道高度增加，传感器的地面覆盖宽度增加，但分辨率降低，因此要根据云图的覆盖和分辨率要求，确定载荷的设计参数，如红外相机的视场、焦距等，卫星轨道决定了星体的光照条件，这会影响电源系统的设计，要结合卫星的功率需求确定太阳帆板的尺寸和定向方式；还会影响热控系统设计，要分析卫星吸收的太阳辐射能量，确定热控系统方案。还要分析卫星轨道的受摄运动，制定轨道保持策略，根据卫星寿命要求，确定轨控系统方案和燃料装载量。2

卫星轨道直接影响发射方案，发射窗口的分析与计算、飞行程序的设计、入轨精度分析、轨道捕获策略制定等都与卫星轨道相关。卫星轨道还影响测控方案设计，要分析可测控条件、计算可测控弧段，根据测控精度要求，确定测控方案。卫星发射入轨后，首先要进行轨道捕获，消除发射误差，使卫星能在标称轨道运行。卫星正常工作后，要不断进行轨道确定，支持卫星云图判读；分析轨道受摄运动，当实际运行轨道与标称轨道偏离过大时，进行轨道保持；开展轨道预报，若发现存在与微流星体或轨道碎片撞击的风险，为避免损毁卫星，可能要实施轨道机动。2