[科普中国]-结构函数

定义

结构函数这一概念是前苏联人德罗兹多夫和塞普列夫斯基首先提出来的,已经被许多国家运用于气象台站网 的设计,普遍认为任一气象要素的结构函数是描述该要素场的统计结构最合适的特征值之一。

同样,结构函数对于描述大气环境中某污染物的浓度场分布也是适合的。

结构函数的定义：设想有 A 、B两个测点 , 相距为L,它们各自有一组监测值A,和Bi , 实际上在监测值之中已包 含了这两点污染物真实的浓度值ai和bi、以及相应的观测误差αi和βi, 即 :

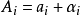
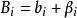
若用这二组数据计算各自的平均值和均方差先必须要知道C点的内插值的误差是多少？我们在这里引入了一个 内插标准误差的概念 , 令其为 E ( L ) , 理论分析表明 , 当 C 点处于 A 、B中点时 , C 点的内插误差最大 , 并可用下 式计算 :

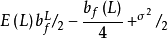
式 中δ²/2称监测随机误差的平方 。
这里用 bf( L )即由真实的污染物浓度计算而得的结构函数来估计内插的误差 , 若用模式计算的浓度场来计算误差 , 则计算值中不含有测量误差。1

方法原理根据模式计算或实测结果得到城市大气污染物浓度场分布,求出结构函数b:(L),再算出内插标准误差E(L)与距离L的变化关系,作出变化图形,然后给出适当的误差范围,即可从标准误差曲线上决定出设站的最佳空间距离,再根据计算出的站网设置的最佳距离,城市大气污染物浓度场分布特征和城市地形、地貌、气象特征,确定出最佳设站个数。

关键是如何选定允许的误差范围,这主要取决于监测本身的精度。从理论上讲,监测的精度应该是越高越好,但要保证很高的监测精度,就必须设很多很密的测点,取得大量的监测数据,这不可能也没有必要。我们认为只要优化点位的精度达到原有的监测精度,而使优化点位的代表性和合理性更好就行了。可以利用Bf(L)=bf(L)+2δ²估计监测的精度。从目前已有测点的监测数据计算出Bf(L),然后将其延长到L=o处,即可得到a。的估计值,由公式推导可得Ek(L)