[科普中国]-超长期预报

定义

超长期预报是指1 年以上的旱涝趋势和冷暖趋势的预报。由于在大尺度时空下这些统计特征参数或概率分布是稳定的，超长期预报因而是可能的。1

超长期预报属于研究气候变迁的范畴，对国民经济计划的编制有重要参考价值。

预报方法重建时间序列由于树木生长过程是受外部环境因子影响的，而气候要素的影响往往是变化最大、最为敏感的。因此，某种树木有可能成为外部气候要素变化的记录器。树木年轮含有精确的定年，更有助于从树木年轮生长状况获取逐年气候变化信息，并进一步转化成可信的代用气候资料。1

树木径向生长除了受各种环境因子影响外，还有自身生长规律。树木随年龄增长而引起的径向生长量的改变,称为树木径向生长“年龄趋势”。由于我们目的是分析树木年轮宽度与气候的关系，因此，必须先估计出年龄趋势，再从年轮宽度序列中将年龄趋势剔除(即生长量订正)。这步工作的方法之一是用该地区该树种大样本平均的年轮宽度曲线作为年龄趋势的标准线，来进行订正。其订正公式为：

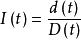
式中：d(t)为需要订正的样本年轮宽度序列：D(t)为标准年轮宽度序列；I(t)为订正后的样本年轮指数序列；t 为树龄。

对单点的树木年轮宽度序列，通过定年构成一个年轮年表。当证实该年表的逐年变化与某气候要素的变化息息相关时，那么，通常就可以设法建立统计模式,以气候要素为预报量(y)，以与树木生长有关的要素为预报因子(x)建立预报方程。

当某已知气象要素(y)与年轮宽度(xi)已剔除年龄因子)的相关性相当好，其相关系数值超过a=0.01的信度水平,就可以尝试用这种回归方程进行过去气候要素的再现。由于树木年轮生长状况可视为前期生长与该年气候影响的共同结果，因而，在建立回归方程时，将其前一年(xt-1)，前两年(xt-2)或前三年(xt-3)的年轮宽度指数值与当年生长(xt)同时作为预报因子，共同建立某个气候要素(yi)为预报量的回归方程：

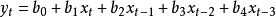
其中b0,b1,b2,b3,b4均为回归系数，然后就可以根据各预报因子对方差贡献大小或标准回归系数大小决定因子的取舍，从而确定气候要素与年轮指数的关系。根据这个关系就可用树木年轮资料重建过去某气候要素的时间序列。1

正交化筛选建模设一维时间序列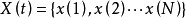建立以均生函数为基础函数的预报模型。1

先对原序列x(t)进行规格化

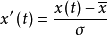
对规格化数据计算x'(t)的均生函数，然后进行Gram-Schmidt正交化处理，用正交化序列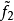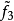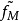，，…，。作为自变量与x(t)建立线性模型

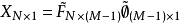
求最小二乘解

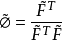
用双评分准则筛选均生函数，最后，制作预报。

由于上面所求的方程系数是由正交均生函数确定的。因此，还必须求出原均生函数fi(t)的系数才能用于制作预报。设筛选出均生函数个数为k，那么，x(t)与fi(t)之间的关系可由线性回归模型表示：

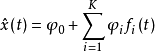
其中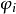称为原系数。

将均生函数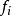作q步周期性外延，由

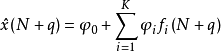
q=1,2,…

即可得到q步预报。

最后对模型的计算值及预报值用第一步的算式进行复原。1

综合预报对时间序列X（t），用三种不同方法：

（1）方法一：趋势分析+方差分析+自回归，

（2）方法二：趋势分析+谐波分析+自回归，

（3）方法三：基于均生函数的正交化筛选建模的拟合（预报）值进行多元回归，用此回归方程进行综合预报。1