[科普中国]-兰贝特定律

简介

用斯蒂芬-波尔兹曼定律，只能计算绝对黑体表面所辐射的总能量，而并不能说明在半球空间各个方向上发射的辐射能量是如何分布的。兰贝特定律则定量地描述了这一分布规律，即黑体表面向它上面的半球空间给定方向上发射的辐射能量，等于它向法线方向上发射的辐射能量与给定方向和法线方向夹角的余弦的乘积。1

定理内容兰贝特定律——定向辐射强度与方向无关。给出了黑体辐能按空间分布的规律。

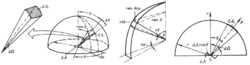公式表示：L（θ）=L=常数1

推导兰贝特定律是描述黑体辐射能量随空间(方向)分布规律的定律，其具体内容如下黑体表面向θ方向发射的定向辐射力：

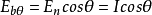
式中为发射辐射的方向θ与表面法线的夹角;Ebθ为黑体表面向θ方向发射的定向辐射力;Ebn为黑体表面法线方向上的定向辐射力，其值最大;Ibθ为黑体表面θ方向上的辐射亮度;Ibn为黑体表面法线方向上的辐射亮度。在此处，因黑体向各方向发射的辐射亮度均相等，故：Ibn=I=Ibθ；由定义可知Ebn=Ibn，于是Icosθ=Ebθ。

对2n空间求积分可得:

E=Iπ

上式表明，黑体表面辐射能量随空间(方向)分布遵循余弦规律，即表面法线方向上辐射能量值最大，切线方向上为零，其余方向由cosθ决定，故兰贝特定律又称余弦定律。1

应用一般地讲，对于一个表面的辐射模型，兰贝特定律是十分近似的。如果一个表面严格遵循兰贝特定律，则相对于此表面任何一个角度上所测得的辐射流，都可用来计算其总的球向辐射流。

在半球空间的各个方向上，辐射亮度Iθ均相等的表面，称为漫辐射面，也称为各向同性表面，故对漫辐射面而言，兰贝特定律成立。2