[科普中国]-差异系数

概念解释

相对差异量数中的一种测度，又名“变异系数”，通常以CV代表之。在统计中，两极差、四分位差、平均差和标准差都属于绝对差异量数。这种差异量数具有与原始资料相同的单位，可用以比较两种差异量的大小。但遇到两种资料的单位不同，或资料的单位相同，而平均数相差甚大时，仍用绝对差异量进行比较，其所得结果则往往不可靠。在这种情况下，则必须使用差异系数。差异系数由于是相对差异量数，它既可用于不同单位资料的差异比较，也可用于不同水平的同类现象的差异情况的比较。最常用的差异系数是由皮尔逊(Pearson，K.)所提出的。所谓差异系数就是以平均数去除标准差再乘以100%，化成百分比的形式。其计算公式为：

式中S为标准差，M为平均数。2

差异系数通常用用标准差计算，因此，差异系数也被称为标准差系数。其计算公式为：

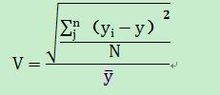
离散系数大，代表其数据的离散程度大，其平均数的代表性就差，反之亦然

常用比较常用于两个方面相对差异量的比较。一是不同质的测量，例如身高与体重各自变异大小的比较，不能直接用标准差，因为二者测量单位不同，而应根据各自的平均数与标准差计算变异系数再比较。二是测量相同，但不同样本的数据相差较大，在这种情况下，一般平均数较大的样本标准差也较大，平均数较小的样本标准差也较小，不能直接用标准差比较变异大小。例如儿童的身高和成人的身高虽然都用长度单位表示，但两样本平均数相差较大，标准差相差也大。欲比较相对差异，都须转换成变异系数。不过相对差异量的比较至今没有检验的方法，只依数值大小作简单的算术比较。变异系数值大变异程度大，反之则小。3