[科普中国]-费马原理

费马原理（Fermat principle）最早由法国科学家皮埃尔·德·费马在1662年提出：光传播的路径是光程取极值的路径。这个极值可能是最大值、最小值，甚至是函数的拐点。 [1] 最初提出时，又名“最短时间原理”：光线传播的路径是需时最少的路径[2]。

费马原理更正确的称谓应是“平稳时间原理”：光沿着所需时间为平稳的路径传播。所谓的平稳是数学上的微分概念，可以理解为一阶导数为零，它可以是极大值、极小值甚至是拐点。

简介费马原理是几何光学的基本定理。用微分或变分法可以从费马原理导出以下三个几何光学定律：

光线在真空中的直线传播。

光的反射定律-光线在界面上的反射，入射角必须等于出射角。

光的折射定律（斯涅尔定律）。

最短光时线可以有多条，例如光线从椭圆面焦点A经过反射到另一焦点B，可以有无数条路径，所有这些路径的光线传播时间都相等。1

光的反射平面反射光从P点出发射向x点，反射到Q点。

P点到x点的距离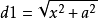，Q点到x点的距离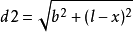，从点P到点Q的光程D为

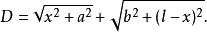
根据费马原理，光线在真空中传播的路径是光程为极值的路径。取光程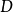对的导数，令其为零：

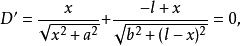但其中：

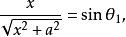
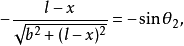即

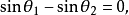
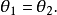
半球面反射球面的半径=R，光线从直径一端Q射向球面，反射到直径另一端P，光程：

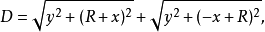因：

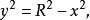所以：

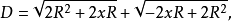根据费马原理：

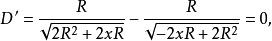解之， 得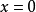，代入D得到：光程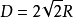，乃是一个最大值=2.8R；（最小值光程是从直径一端到Q另一端P，光程=2R）。2

运动学伯努利家族的约翰·伯努利在解决最速降线问题时曾利用到费马原理。他将小球运动类比作光线的运动，从而得出最速降线为摆线。2

参阅费马

哈密顿原理

最小作用量原理

路径积分表述

惠更斯－菲涅耳原理

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所