[科普中国]-弹性力

弹性物体因外力产生形变后的恢复力，简称弹力。形变也存在于物体内部，因此物体内部的各部分间都有弹性力相作用。弹性力有各种名称：相互压缩时，称压力，垂直于物体表面的压力称法向压力；相互拉长时，称张力。物体给平面或斜面的法向压力的反作用力，称支持力或反力，实质上也是压力。

基本概念弹性物体因外力产生形变后的恢复力 。 简称弹力。形变也存在于物体内部，因此物体内部的各部分间都有弹性力相作用。弹性力有各种名称：相互压缩时，称压力，垂直于物体表面的压力称法向压力；相互拉长时，称张力。物体给平面或斜面的法向压力的反作用力，称支持力或反力，实质上也是压力。一定范围内弹性力和变形程度成正比，这个范围称弹性限度。在限度内，撤去外力，物体能恢复原状；超过这限度，变形程度不再和外力成正比，撤去外力后物体也不能恢复原状。对弹簧来说，弹性力为F=－kx，x表示弹簧终端的位移，k为弹性力和位移值之比，称刚度系数，负号表示弹性力的方向与位移的方向相反。弹性力也是保守力，弹性力作功可用弹性势能表示 ，其值为，x为位移的值。

在外力作用下弹性物体形变后所产生的一种恢复力。 弹性力的特点是它在变形体上所做的功并不转化为热， 但可转化为势能。弹性力是一种保守力。物体中任何两个质点相对位置的变化，称为物体变形。当物体的形变很小时，弹性力F和物体中质点M开平衡位置时的位移成正比,其方向指向力图使质点复到平衡位置的方向。包括风化作用、侵蚀作用、搬运作用、沉积作用和固结成岩作用。指由太阳辐射、重力、日月引力、水流、风力等来自地球外部的营力(通过大气、水、生物等)所引起的作用。来自地球外部，主要是太阳辐射能，包括风化、堆积、侵蚀、搬运固结成岩作用等。1

相关知识弹性力学比较偏重数学，寻求一些特殊问题的解析解答，常采用偏微分方程中的求解方法，对高数要求较高。我们上的弹性力学主要讨论弹性力学数学方法，就是应用数学分析工具建立弹性力学的基本方程和基础理论，并且根据边界条件求解弹性体的应力场和位移场。弹性力学的基本方程，在数学上，是偏微分方程的边值问题，求解的方法有解析法和近似解法。解析法，即直接求解偏微分方程边值问题，这在数学上难度极大，因此仅适用于个别特殊边界条件问题。由于解析方法的应用困难，因此近似解法在弹性力学的发展中有着重要意义。

弹性力学，是固体力学的一个分支，研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。弹性力学的研究对象是完全弹性体，弹性体是变形体的一种，在外力作用下物体变形，当外力不超过某一限度时，出去外力后，除去外力后物体即恢复原状。根据问题的性质，忽略一些很小的次要因素，对物体的材料性质采用了一些基本假定，即弹性力学的基本假定，主要有连续性、完全弹性、均匀性、各向同性，符合以上假定的物体，就称为理想弹性体；此外，假定位移和形变是微小的。物体任意一点的位移，用它在x、y、z三轴上的投影表示。研究讨论的平面应力弹性体的形状为等厚度均匀薄板，厚度方向的尺寸小于其他两个方向的尺寸。在解决弹性力学平面问题时，需要建立基本方程：平衡方程—应力与外力之间的关系；几何方程—位移与应变之间的关系；物理方程—应变与应力之间的关系。以及边界条件的建立，边界条件表示在边界上位移与约束，或应力与面力之间的关系式。位移分量已知的边界，建立位移边界；给定了面力分量，建立应力边界条件。圣维南原理，面力的改变，就只会使近处产生显著的应力改变，而远处的应力改变可以忽略不计。在解决平面问题时，按位移求解平面以及在问题或按应力求解平面问题。以及在直角坐标和及极坐标中建立基本方程和求解方法，弹性力学的学习中，对应变、应力等量的意义有了更深的了解，以及对量的表示方式有所了解。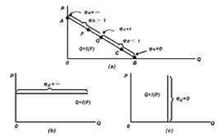

弹性力的基本假设（1）连续性，所有的物理量均可以用连续函数，从而可以应用数学分析的工具；

（2）完全弹性，物体中的应力与应变之间的物理关系可以用胡克定律来表示；

（3）均匀性，物体的弹性常数等不随位置坐标而变化；

（4）各向同性，弹性常数等也不随方向而变化；

（5）小变形假定，简化几何方程，简化平衡微分方程。1

相关原理圣维南原理圣维南原理是基于静力等效原理，当将面力的等效变换范围应用到大边界上，则必然使整个物体的应力状态都改变，所以大边界不能应用静力等效，在大边界上不能应用圣维南原理。

叠加定理在线弹性和小变形假定下，作用于弹性体上几组荷载产生的总效应（应力和变形），等于每组荷载产生的效应之和，且与加载顺序无关。2

虚位移原理假定处于平衡状态的弹性体在虚位移过程中，没有温度的改变，也没有速度的改变，既没有热能和动能的改变，则按照能量守恒定理，形变势能的增加，等于外力势能的减少，也就等于外力所做的功，即所谓虚功。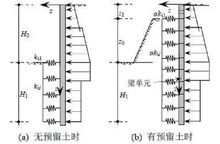

弹性力的研究方法在弹性体区域内部，考虑静力学、几何学和物理学三方面条件，分别建立三套方程。即根据微分体的平衡条件，建立平衡微分方程；根据微分线段上形变与位移之间的几何关系，建立几何方程；根据应力与形变之间的物理关系，建立物理方程。此外，在弹性体的边界上还要建立边界条件。在给定面力的边界上，根据边界上微分体的平衡条件，建立应力边界条件；在给定约束的边界上，根据边界上的约束条件建立位移边界条件。求解弹性力学问题，即在边界条件下根据平衡微分方程、几何方程、物理方程求解应力分量、形变分量和位移分量。

弹性力学中正应力用σ表示，并加上一个下标字母，表明这个正应力的作用面与作用方向；切应力用τ表示，并加上两个下标字母，前一个字母表明作用面垂直于哪一个坐标轴，后一个字母表明作用方向沿着哪一个坐标轴。并规定作用在正面上的应力以沿坐标轴正方向为正，沿坐标轴负方向为负。相反，作用在负面上的应力以沿坐标轴负方向为正，沿坐标轴正方向为负。

平面应力问题是指很薄的等厚度薄板，只在板边上受有平行于板面并且不沿厚度变化的面力，同时，体力也平行于板面并且不沿厚度变化。对应的应力分量只有σx ，σy ，τxy 。而平面应变问题是指很长的柱形体，在柱面上受有平行于横截面并且不沿长度变化的面力，同时体力也平行于横截面并且不沿长度变化，对应的位移分量只有u 和v。1

本词条内容贡献者为:

何星 - 副教授 - 上海交通大学