[科普中国]-频谱密度

频谱就是频率的分布曲线，复杂振荡分解为振幅不同和频率不同的谐振荡，这些谐振荡的幅值按频率排列的图形叫做频谱。设一个能量信号为s（t），则它的频谱密度S（w）可以由傅里叶变换求得。

频谱分析，是信号分析技术中的经典部分。尤其是自FFT信号分析仪得以应用以来，频谱分析技术曾作为信号分析的主流技术而得到空前的发展，在工程领域被广泛应用，解决了大量工程实际问题，即使现代信号分析技术大大发展，频谱分析仍作为传统和经典的信号分析技术而继续被广泛应用，并经常成为其他分析技术的参照。

相关定义频谱的定义任何表现于时间或空间距离上有复杂振动的形式的变量，都可以分解为许多不同振幅和不同频率的谐振，把这些谐振的振幅值按频率（或周期）排列的图形。可用作传送信息的电磁波或振荡的频率集合。

频谱就是频率的分布曲线，复杂振荡可以分解为振幅不同和频率不同的谐振荡，这些谐振荡的幅值按频率排列的图形叫做频谱。广泛应用在声学、光学和无线电技术等方面。频谱是频率谱密度的简称。它将对信号的研究从时域引到频域，从而带来更直观的认识。1

频谱密度的定义设一个能量信号为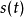，则它的频谱密度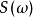可以由傅里叶变换求得：。

能量信号的频谱密度和功率信号的频谱主要区别有：（1）频谱密度是连续谱，而功率信号的频谱是离散谱；（2）频谱密度单位是幅度/频率，而功率信号的频谱单位是幅度；（3）能量信号的能量有限，并连续的分布在频率轴上，每个频率点上的信号幅度是无穷小的，只有df上才有确定的非0振幅；（4）功率信号的功率有限，但能量无限，它在无限多的离散频率点上有确定的非0振幅。

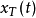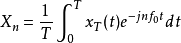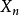基于FT的频谱函数与频谱函数密度周期信号的频谱函数在进行频谱的理论分析时，对周期信号，要用傅氏级数（FS）对其进行处理，得到：，。其中，为周期信号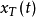的频谱函数。

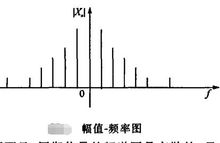在频域坐标系上，幅值-频率图形如右图所示，称为周期信号的频谱图（幅-频图）。由图可见，周期信号的频谱图是离散的，只有在时有值，其幅值与信号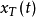具有相同的量纲，且相对应两条谱线（例如n=±3）之和表示该阶谐波（例第三阶）的真实幅值。2

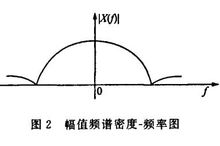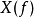周期信号的频谱密度函数对非周期信号，则要用傅式变换（FT）对其进行处理，得到：，。称为信号的频谱密度函数。在频域坐标系上，典型的幅值密度-频率图如右图所示，称为信号的频谱密度图。

由图可见，非周期信号的频谱密度图是连续的。其纵坐标表示信号的幅值密度，而不是谐波的幅值，其量纲是：信号量纲/Hz。

基于FFT信号分析仪上的频谱与功率谱密度FFT谱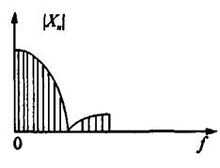FFT信号分析仪的工作原理是离散傅里叶变换，即DFT。对信号进行DFT，实质上包含几个环节：时域采样（时域离散化）、时域截断（加窗）和频域采样（频域离散化）。根据傅氏变换的性质，在频域采样过程中，实际上是对时域信号的周期化。即此时参与变换的信号不再是原信号，而是以窗宽T为周期的信号。既然是周期信号，经变换后所得到自然是该信号的频谱函数，称之为信号的FFT谱或线性谱。典型的FFT谱如右图所示（单边显示）。

与周期函数的频谱图相似，信号的的FFT谱是离散的，其幅值具有与信号相同的量纲。

功率谱由于是复函数，在工程应用中不够方便，为此常将其与复共轭相乘，得到其功率谱（PowerSpectrum），即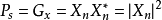，其中：是的复共轭。功率谱Ps是实函数，是的平方，不仅使用方便而且其特征更加突出。

功率谱密度当采用不同的频率分辨率进行信号分析时，尽管对其某一信号的功率谱具有相似的波形，但其各点的功率谱值却是不同的，越大，所得到的功率谱值也就越大。这样不便于采用不同分析频段（亦不同）时所得结果间的比较。于是，在信号分析仪上又定义了功率谱密度的概念，即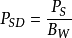：，式中，为等效滤波器带宽，是用频率分辨率乘以所选窗函数的窄带修正因子。对于矩形窗、力窗和指数窗，=。

能量谱密度在某些工程中，还要用到能量谱的分析，于是在信号分析仪中又定义能量谱密度，即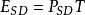：，其中：T为所分析信号的时间记录长度。

总结（1）当对信号进行基于FT的理论分析时，对周期信号傅氏分解，得到其离散化的频谱函数。而对非周期信号，应用傅氏变换，得到的是信号的频谱密度函数。

（2）当使用FFT信号分析仪进行信号分析时。由于DFT的周期化处理，所得到的是信号的频谱函数，而并非频谱密度函数。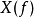

（3）在信号分析仪上，功率谱密度是根据频谱函数的运算而得到的，是为了方便工程运算结果的比
较，与理论分析中的频谱密度函数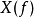不同。3

本词条内容贡献者为:

耿彩芳 - 副教授 - 中国矿业大学