[科普中国]-一阶偏微分方程

一阶偏微分方程是最简单的一类偏微分方程。一阶偏微分方程的几何理论有悠久的历史渊源，以后经过É.(-J.)嘉当等人的发展，在几何学、力学和物理学中都有重大的意义。

定义函数所包含的偏导数的最高阶数称为偏微分方程的阶。如果函数中 u 的偏导数只是 u 的一阶偏导数，则称该方程为一阶偏微分方程。

偏微分方程[partial differential equation]

偏微分方程是包含未知函数及其偏导数的方程。如果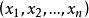是自变量，以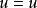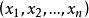为未知函数的偏微分方程的一般形式是

这里 F 是它的变元的函数， 为非负整数，。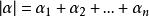

F 所包含的偏导数的最高阶数称为偏微分方程的阶。如果 F 中 u 的偏导数只是 u 的一阶偏导数，则称该方程为一阶偏微分方程。

如果 F 中 u 的最高阶偏导数是二阶，则称该方程为二阶偏微分方程（partial differential equation of higher order）。

如果一个偏微分方程中，未知函数及其所有各阶偏导数以线性形式出现，则将这个偏微分方程称为线性偏微分方程（linear partial differential equation），反之，则称为非线性偏微分方程（nonlinear partial differential equation）。

若一个非线性偏微分方程中，未知函数的所有最高阶偏导数以线性形式出现，而其系数含有该未知函数或其较低阶的偏导数，则称这样的非线性偏微分方程为拟线性偏微分方程（quasilinear partial differential equation）。

又若一个非线性偏微分方程中，未知函数的所有最高阶偏导数以线性形式出现，且最高的阶偏导数的系数也不含未知函数与其较低阶的偏导数，这样的非线性偏微分方程称为半线性偏微分方程（semilinear partial differential equation）。1

应用一阶偏微分方程的几何理论有悠久的历史渊源，以后经过É.(-J.)嘉当等人的发展，在几何学、力学和物理学中都有重大的意义。

偏微分方程研究各类偏微分方程的求解与解的性质。在18世纪初，微积分理论形成后不久，人们就开始结合物理问题研究偏微分方程，并逐渐形成一个独立的数学分支。最早研究的几个偏微分方程是弘振动方程、热传导方程和调和方程。随着力学、物理学的发展，连续介质力学、电磁场论、量子力学、引力理论、规范场论等方面的基本规律都被写成偏微分方程的形式。数学领域中分析学、几何学中很多基本问题也可归结为一些偏微分方程的求解。近年来，在各门自然科学、工程技术以致金融、经济、社会学等学科中又不断归结出一些新的偏微分方程，它们的研究对于相应学科的发展是十分重要的。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学