[科普中国]-交通分配

静态交通分配

一般的交通分配，OD矩阵是已知且确定的，不考虑其随时间的变化，因此称为静态交通分配。

静态交通分配的前提条件是：1

(1) 路网拓扑空间结构已知；

(2) 路网特性、路段旅行时间函数已知；

(3) 动态的时变交通需求已知；

(4) 出行者具有交通路网及交通状况的全部信息，而且能够持续做出正确选择；

(5) 所有出行者的路线选择准则相同；

在此前提条件下，交通分配就是求解路网中各路径的交通流量，以对路网性能进行评价。

动态交通分配动态交通分配是在交通供给情况以及交通需求状态已知的条件下，分析其最优的交通流量分布模式，通过一定的控制手段和诱导策略在空间、时间尺度上重新合理配置人们已经产生的需求，从而使交通路网得以高效运行。1

右图为交通控制、诱导与分配之间的关系图: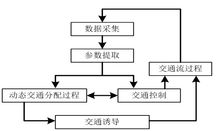此图表明了动态交通分配模型在交通诱导与控制中的位置。由图可以看出，动态交通分配为交通流管理与控制、动态路线诱导等提供了依据，而交通与诱导则是动态交通分配的实现过程。交通控制通过改变路口的信号配时方案来改变车流的时间分布；而动态路线诱导则通过信息提供、车载诱导系统等非强制性手段改变车流的空间分布。1

动态交通分配模型的分类**（1）根据描述交通流方法的不同，可将动态交通分配模型分为仿真模型和分析模型。**

仿真模型中，交通流过程用仿真网络的运行来代替，其路段特性，如费用、走行时间等通过计算机模拟的动态网络加载获得。基于分析的动态交通分配模型则是通过数学函数关系来描述路网的动态特性。仿真模型从分析、模拟出行者的出行选择行为出发，便于集成各种控制策略，分析各个控制策略的效用，同时，使用这种方法不必求出各路段特性函数的具体形式，也不必对模型的参数进行辨识，这是其优点所在。但仿真模型分析能力差，不能从模型本身分析其解的收敛性，以及模型的精度和灵敏度。因此基于仿真模型的动态交通分配模型更适于工程应用。分析模型结构严谨、逻辑严密是其优点所在，但是分析模型为止仍然缺乏行之有效的算法。并且由于交通系统本身的复杂性和不确定性使得无法用一个简单的数学形式来精确描述网络的所有动态特性。在建立分析模型过程中，还往往对模型本身附加了许多理解化的条件，所以分析模型还停留在理论研究阶段，更适用于学术探讨。1

（2）根据描述模型的数学手段的不同，可将动态交通分配模型分为数学规划模型、最优控制模型和变分不等式模型(Variational Inequality，简称VI模型)。

数学规划模型是在静态交通分配向动态交通分配过渡的过程中产生的，由于受到求解的凸规划条件和动态交通分配的FIFO(First-in-First-out)规则的限制，不能由单讫点网络扩展到多讫点网络，因此已很少应用。在静态交通分配模型中，用户均衡是一种真正的均衡状态，同时也达到了用户均衡。在静态情形下，用户均衡与用户均衡是统一的，但在动态情形下二者并不能统一，而且均衡本身就是一种静态概念，系统总是在动态运行中趋于均衡，但却总是无法达到均衡。正是由于趋于均衡的内因，系统才呈现出动态的现象。因此，在动态交通分配中，运用均衡的概念是不准确的，而应该应用最优化的概念，即动态用户均衡。交通流寻求均衡的过程也就是一个最优控制的过程，因此，最优模型近年得到了众多学者的青睐。VI模型是基于路线选择与网络加载的结合，这两个过程都是基于路线的。对于所有基于路线的模型，在求解的过程中由于涉及路线的枚举过程，因此适应于小型的简易网络，而且由于路线与路段流之间存在多对一的关系，这增加了VI模型实用的难度。1

（3）根据模型是否满足均衡原理，动态交通分配模型分为均衡模型和非均衡模型。

动态交通分配模型分析简述动态交通分配是在交通供给状况以及交通需求状况均为已知的条件下,分析其最优的交通流量分布模式,从而为交通流管理、动态路线引导等提供依据。因此，动态交通分配的首要前提是对每时每刻产生的出行需求用其分布的正确把握，在确知动态时变交通需求的基础之上，再对其进行正确的分配。由于交通出行的目的性决定了OD矩阵在动态交通分配中的重要作用，因此在分配中假定OD矩阵是可以获取的已知确定量。除了已知时变交通需求以外，路网结构和动态特性也是必需的。在动态交通分配模型中，出于模型建立和求解的需要，往往假定路段旅行时间和路段流出率是路段流量的函数，还假定路段之中产生车辆发生在路段末端节点，路段之中吸收车辆发生在路段始端节点，这样车辆的吸收与产生只发生在节点处，路段之中不吸收和产生车辆。1