[科普中国]-克劳修斯-莫索提方程

克劳修斯-莫索提方程是关于解释分子α的极化性与介电常数ε（在这种极化性中由分子组成的电介质物质）的关系。

简介克劳修斯-莫索提方程（Clausius-Mossotti equation）表达了线性介电质的极化性和相对电容率之间的关系，是因意大利物理学者莫索提（Ottaviano-Fabrizio Mossotti）和德国物理学者鲁道夫·克劳修斯而命名。1这方程式也可以更改为表达极化性和折射率之间的关系，此时称为洛伦兹-洛伦茨方程式（Lorentz-Lorenz equation）。

极化性是一种微观属性，而相对电容率则是在介电质内部的一种巨观属性，所以，这方程式式连结了介电质关于电极化的微观属性与巨观属性。

导引一个分子的极化性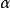 定义为

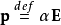
其中，p是分子的感应电偶极矩，E是作用于分子的电场。

介电质的电极化强度定义为总电偶极矩每单位面积：

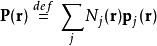
其中，P是电极化强度，r是检验位置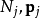， 分别是分子j的数量每单位面积与电偶极矩。

总合介电质内每一种分子的贡献，就可以计算出介电质的电极化强度。将极化性的定义式代入，可以得到

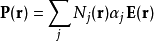
当计算这方程式时，必需先知道在分子位置的电场，称为“局域电场”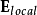 。介电质内部的微观电场，从一个位置到另外位置，其变化可能会相当剧烈，在电子或质子附近，电场很大，距离稍微远一点，电场呈平方反比减弱。所以，很难计算这么复杂的电场的物理行为。幸运地是，对于大多数计算，并不需要这么详细的描述。所以，只要选择一个足够大的区域（例如，体积为V'、内中含有上千个分子的圆球体V '）来计算微观电场 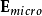的平均值，称为“巨观电场” 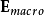，就可以足够准确地计算出巨观物理行为：

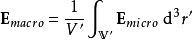
对于稀薄介电质，分子与分子之间的距离相隔很远，邻近分子的贡献很小，局域电场可以近似为巨观电场 ：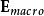

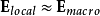
但对于致密介电质，分子与分子之间的距离相隔很近，邻近分子的贡献很大，必需将邻近分子的贡献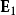 纳入考量：

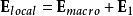
因为巨观电场已经包括了电极化所产生的电场（称为“去极化场”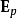），为了不重复计算，在计算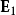时，必需将邻近分子的真实贡献减掉去极化场：

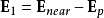
举一个简单案例，根据洛伦兹关系（Lorentz Relation），对于立方晶系结构的晶体或各向同性的介电质，由于高度的对称性，。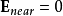

现在思考以分子位置r为圆心、体积为V'的圆球体V'，感受到外电场的作用，V'内部的束缚电荷会被电极化，从而产生电极化强度P。假设在V '内部的电极化强度P相当均匀，则电极化强度P与V'的电偶极矩之间的关系为

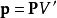
这线性均匀介电质圆球体内部的电场为

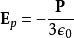
综合前面得到的结果：

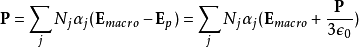
对于各向同性、线性、均匀的介电质，电极化率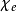定义为

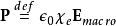
电极化率与极化性的关系为

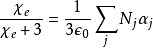
由于相对电容率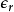与电极化率的关系为

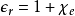
所以，电容率与极化性的关系为

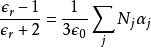
这方程式就是克劳修斯-莫索提方程式。

电介质的折射率n为

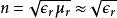
其中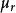，是相对磁导率。

对于大多数介电质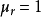，，所以，折射率近似为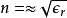。将折射率带入克劳修斯-莫索提方程式，就可以给出洛伦兹-洛伦茨方程式：

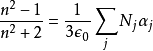
参阅折射率

铁电性

低介电常数材料

高介电常数材料(High-k)

居里点

驻极体

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所