[科普中国]-瑞典条分法-

一般计算公式

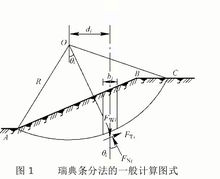瑞典条分法假设滑动面为圆弧面，将滑动体分为若干个竖向土条，并忽略各土条之间的相互作用力。按照这一假设，任意土条只受自重力FWi、滑动面上的剪切力FTi和法向力FNi，如右图1所示。将FWi分解为沿滑动面切向方向分力和垂直于切向的法向分力，并由第i条土的静力平衡条件可得FNi=FWicosθi，其中，FWi=bihi×γi。

设土坡安全系数为Ks，它等于第i个土条的安全系数，由库仑强度理论有

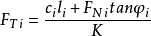
式中，FTi———土条i在其滑动面上的抗滑力；

Ks———土坡和土条的安全系数。

按整体力矩平衡条件，滑动体ABC上所有外力对圆心的力矩之和应为0。在各土条上作用的重力产生的滑动力矩之和为

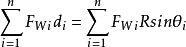
滑动面上的法向力FNi通过圆心，不引起力矩，滑动面上设计剪力FTi产生的滑动力矩为

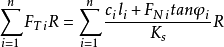
由于极限情况下抗滑力矩和滑动力矩相平衡；所以令上述两式相等，则

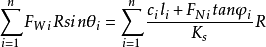
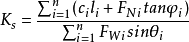式①

这是最简单的条分法的计算公式。由于忽略了土条之间的相互作用力；所以由土条上的3个力FWi、FTi和FNi组成的力多边形不闭合，所以瑞典条分法不满足静力平衡条件，只满足滑动土体的整体力矩平衡条件。尽管如此，由于计算结果偏于安全，在工程上仍有很广泛的应用。

需要指明的是，使用瑞典条分法仍然要假设很多滑动面并通过试算分析，才能找到最小的Ks值，从而找到相应的最危险的滑动面。1

有孔隙水压力作用时土坡稳定分析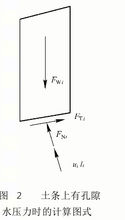当已知第i个土条在滑动面上的孔隙水压力为ui时（如图2所示），要用有效指标c′i及φ′i代替原来的ci和 φi。考虑土的有效强度，根据摩尔-库仑强度理论，有

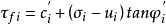
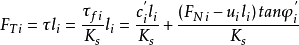式②

取法线方向力的平衡，可得

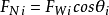
各土条对圆弧中心O的力矩和为0，即

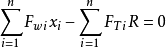
式中，xi———圆心O至FWi作用线的水平距离，xi=Rsinθi。

将式②代入式得

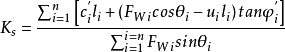
这就是用有效应力方法表示的瑞典条分法计算Ks的公式。

经过多年工程实践，对瑞典条分法已积累了大量的经验。用该法计算的安全系数一般比其他较严格的方法低10% ～20%；在滑动面圆弧半径较大并且孔隙水压力较大时，安全系数计算值估计会比其他较严格的方法小一半。因此，这种方法是偏于安全的。

坡顶有超载和土成层时稳定性分析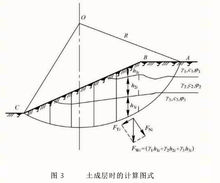当土坡由多层土构成（如图3所示），在使用公式①时应作必要的修正。

（1）如果同一土条跨越多层土，计算其重量时应分层取相应的高度和厚度，计算相应重量后叠加。如第i个土条包括k层土，则

FWi=bi（γ1ih1i+γ2ih2i+…+γkihki）

（2）计算滑动面上的抗剪强度时，所用的土性参数c、φ应按土条滑动面所在的具体土层位置来选取相应的数值。如当第i个土条的滑动面在第m层内时，则

FTfi=cmilmi+FNitanφmi

当第i个土条的滑动面跨越m层土，则

FTfi=（c1il1i+c2il2i+…+cmilmi）+FNi（tanφ1i+tanφ2i+…+tanφmi）。

提示：FNi是第i条土滑动面上的法向反力之和，FNi=FWicosθi，与土条自重有关，而与滑动面上土层土性没有直接关系。因此，对于成层土坡，可用下式计算其安全系数：

式中，FTi=FWisinθi

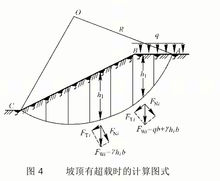如果在土坡坡顶作用着超载q，如图4所示，计算的基本原则和程序不变，只是在土条受力分析时，需要将土条上作用的超载加进土条的自重中去考虑；如果超载作用在坡面上，处理方法相似。当然可能某些土条上并没有超载，则该土条仅考虑自重。当仅在坡顶有超载时，按下式计算安全系数，即

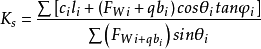
用条分法时简单土坡最危险滑动面的确定简单土坡指的是土坡坡面单一、无变坡、土质均匀、无分层的土坡。如图5所示，这种土坡最危险的滑动面可用以下方法快速求出。

（1）根据土坡坡度或坡角β，由下表查出相应 α1、α2的数值。

（2）根据α1角，由坡脚A点作线段AE，使角∠EAB=α1；根据 α2角，由坡顶B点作线段BE，使该线段与水平线夹角为α2。

（3）线段AE与线段BE的交点为E，这一点是 φ=0的粘性土土坡最危险的滑动面的圆心。

（4）由坡脚A点竖直向下取坡高H值，然后向右沿水平方向线上取4.5H，并定义该点为D点。连接线段DE并向外延伸，在延长线上距E点附近，为 φ >0的粘性土坡最危险的滑动面的圆心位置。

（5）在DE的延长线上选3～5个点作为圆心O1、O2、O3…，计算各自的土坡稳定安全系数K1、K2、K3…。而后按一定的比例尺，将Ki的数值画在过圆心Oi与DE正交的线上，并连成曲线（由于K1、K2、K3…数值一般不等）。取曲线下凹处的最低点O′，过O′作直线O′F与DE正交。O′F与DE相交于O点。

（6）同理，在O′F直线上，在靠近O点附近再选3～5个点，作为圆心O′1、O′2、O′3…，计算各自的土坡稳定安全系数K′1、K′2、K′3…。而后按相同的比例尺，将K′i的数值画在通过各圆心O′i并与O′F正交的直线上，并连成曲线（因为K′1、K′2、K′3…数值一般不等）。取曲线下凹处的最低点O″点，该点即为所求最危险滑动面的圆心位置。2

|| ||