[科普中国]-反常扩散

介绍定义

作为一个随机过程，布朗微粒的正常扩散是中心极限定理的直接结果，该输运过程遵循统计表现为其均方位移与时间的线性依赖关系：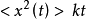

其中k为扩散系数，然而许多复杂系统的扩散过程通常不再遵循高斯统计，即Fick第二定律不能够描述相应的输运行为这种现象被称为反常扩散（anomalous diffussion)。

大量的实验表明，反常扩散现象在自然界中普遍存在，该现象在物理、化学、生物等领域的各种复杂系统中被频繁观测到，不同于经典扩散，反常扩散不再遵守Fick定律或Fourier定律，反常扩散微粒的均方位移表现为与时间的非线性依赖关系：

分类其中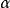 为反常扩散指数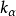， 为反常扩散系数，根据反常扩散指数，反常扩散分为次扩散、正常扩散、超扩散、弹道扩散。特别地，来源于粒子与热浴之间的相互作用，其均方位移是发散的，也是反常扩散的一种情形。

描述方法近年来，反常扩散现象引起人们的广泛关注经典的扩散表现为布朗微粒的局域性运动，而反常扩散则表现为布朗微粒的非局域性（时间和空间）运动大量有效的方法和模型被用来描述这一现象。

主要包括：分数布朗运动、广义的扩散方程、连续时间随机行走模型、Langevin方程、广义的Langevin方程、广义主方程方法、Tsalli统计等，上述描述反常扩散的方法和模型中，只有连续时间随机行走模型和广义的Langevin方程结合了系统的记忆性质且其概率密度函数均有一致的表达式虽然连续时间随机行走模型清晰地描述了粒子的运动轨迹，但是该模型只与系统的统计性质有关，不涉及系统的动力学行为且该模型无法直接引入力场和边界（或无法直接在相空间中考虑所研究微粒的动力学行为作为描述反常扩散动力学的另一个合理选择，分数阶动力学方程则可以直接引入外力场并能灵活地处理边界