[科普中国]-角分辨率

定义

角分辨率是指成像系统或系统的一个部件的分辨能力。即成像系统或系统元件能有差别地区分开两相邻物体最小间距的能力。分辨本领一般用成像系统对两个最小可辨目标之间所张角度大小表示，通常用测度角的弧度系统描述，亦称角分辨本领（或角分辨率）。分辨本领亦可用单位长度的线对数（线对/毫米）表示。角分辨本领（毫弧度）与分辨本领（线对/毫米）可在一定条件下相互转换（换算）。

光学中的像分辨本领在光学里而，像分辨本领是指仪器分辨开相邻两个物点的像的能力。实际应用时，有二个判据来判断两点的像是否能被分开。1

（1） 瑞利判据：对于强度相同的两点光源，如果一个物点的衍射图样中央主极大，与另一个物点的衍射图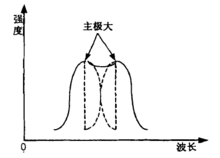样中央主极大旁的第一极小相重合时（见图），这两个物点是恰可分辨的。

（2）泰勒判据：当两波氏成分的强度曲线在半强度点相交，使得合成曲线鞍点的强度等于任一波氏成份的主极大强度时，这两个波氏是恰可分辨的（见图）。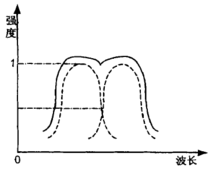

（3）斯帕劳判据：当两衍射图样的合成强度曲线中的鞍点刚刚消失时，两点恰能被分辨。

谱估计分辨率在谱估计中，通常是用白噪声中双正弦的分辨特性来评价不同谱估计方法的分辨率。玛坡耳和弗罗斯特对此作了定量讨论，并给出了谱估计分辨率的定义。2

设有两个正弦信号，频率分别为f1和f2，它们之间并无其它信号。当附加有白噪声时，其功率谱如图所示，具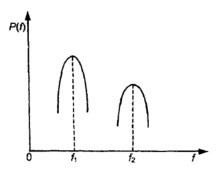有两个明显的峰值，称两正弦信号能被良好地分辨。

若两信号频率逐渐接近，在频谱图上表现为代表信号的两峰越靠越近，慢慢融合为一，则它们不再能被分辨。当两谱峰逐渐靠近，使得两峰之间由于叠加引起的谱估计值逐渐增大，同时满足以下两个条件时：

且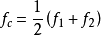

玛坡耳认为两正弦信号刚能被分辨，参见图，并将此时的频率间隔定义为这种谱估计法对两正弦信号的分辨率。

对于以上的判据，一般是已知两个像或谱峰的原形，在它们逐渐靠近时判断是否能被分辨，这是很好理解的。而MUSIC用于雷达中是直接得到已经重叠后的像，不知道它们的原形如何，只知道峰值位置所在。因而无法判断主极大旁的第一极小，也不知道鞍点在哪，这使我们给不出恰好可分辨的界限。

基于MUSIC算法的理论角分辨率提取海洋表面径向流速需分离出多普勒谱的一阶谱区。一阶谱区内相对于正负Bragg频率的不同频偏对应于大小不同的流速。MUSIC估计径向流到达角时，是针对每一个确定的流速，形成一个数据矩阵，再从中求出这一流速对应的方位角。必须考虑到分离一阶谱区时所需的阈值信噪比（即高于此信噪比的信号才是可用的），以及系统的相干积累时间对角分辨率造成的影响。3

在其它条件（如相干积累时间）固定的情况下，阈值越小，则一阶谱区越宽，谱区中对应的流速就增多，显然判断出的方向总数也越多，角分辨率会相应提高。但阈值过低会带来虚假流速，或使MUSIC算法提取的海流方位因过低的信噪比出现较大的误差。

海洋表面流是连续分布的，预先并不知道出现在雷达回波中的海流来自哪个方向。对于相邻海域的两个流速，实际上只存在两种情况，流速相同和流速不同。所以，基于MUSIC算法的理论分辨率也应分成两种情况来讨论。

1、相邻海域流速不同:这时代表两海流方位的谱峰分别出现在不同的空间谱中，即两海流回波到达角的求得是相互独立的过程，当两个海流不相干的情况下，它们的谱峰可以无限接近（实际考虑到海洋动力学，Barrick认为两个海流只有相隔2o以上才能认为是不相干的）。由于样本数和信噪比等因素的影响，MUSIC算法求出的到达角会出现扰动（相对于实际到达角）。

2、相邻海域流速相同:这时代表它们方位的谱峰将出现在同一空间谱中，相互之间有所影响，即使在理论上两回波到达角也不可能无限接近。

雷达的角分辨率角分辨率实际上指的是雷达的指向精度，比如雷达指向精度0.01弧度（换算成角度就是0.6度），那么就可以在100米的距离获得1米的分辨率，如果雷达的指向精度是0.001弧度的话，那么就可以在1000米的距离获得1米的分辨能力。

雷达的角分辨率与雷达的波长成反比，与天线的直径或者叫孔径成正比，就是说波长越长，分辨率越低，孔径越大，分辨率越高。

X波段雷达使用的频率是8-12吉赫兹，波长3厘米左右，分辨率比C、E、F等波段高，比Ka波段和毫米波段的雷达分辨率低。