[科普中国]-地心引力常数

引力常数

引力常数分为万有引力常数、高斯引力常数和地心引力常数等，这些引力常数被应用于物理学、天文学和地球物理学的各种实验测量中。万有引力常数是牛顿万有引力定律公式中的常数，一般用G表示；高斯引力常数用k表示，k2=G；地心引力常数用GM表示，单位为m3/s2，GM=G·M，M为地球质量。虽然它们的物理意义各不相同，但它们之间都有一定关系。按物理常数的定义，它们应是不变的，可是早在20世纪30年代前狄拉克就已提出万有引力常数G随时间而变化，以后好多学者都在理论上预测和实验中观测了G的变化值。此外，近年来，人们根据对人造卫星运动和飞向月球的火箭加速运动的观测分析，指出地心引力常数也随时间变化着。2

地心引力常数的观测值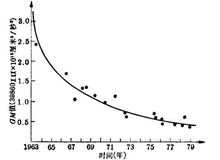1964年召开的第12届国际天文学协会通过的天文常数中，包括地心引力常数一项，当时采用的数值是GM=398603×109m3/s2。后来这个数值在1967年的国际测地和地球物理学协会上，列为“测地参考系统”的基本数据之一。从1968年起，世界各国都应用这个数字，计算天文年历以及人造卫星和月球火箭等的运动。3

国际大地测量与地球物理联合会第16届大会地心引力常数的推荐值为（3986005±3）×108m3/s2（含大气层）；国际大地测量与地球物理联合会第17届大会地心引力常数的推荐值为（39860047±5）×107m3/s2（含大气层）；国际大地测量与地球物理联合会第18届大会地心引力常数的推荐值为（39860044±1）×107m3/s2（含大气层）。

通过近十几年来较为精确的测量，发现GM值有逐年下降的趋势。为了得到表征这种变化的规律，利用1963~1979年由各种方法测得的、标准误差小于0.8km3/s2的GM值进行最小二乘法拟合，其变化如图。4

地心引力常数变化特点及原因近年来，通过对飞向月球的火箭加速运动的观测分析，发现地心引力常数呈逐年下降趋势。下表列出了国际天文协会（IAU）给出的一些年份的GM值。

|| || 地心引力常数的测定值

由以上观测数据可知，GM值的变化有以下2个特点：

（1）GM值呈逐年下降趋势，如果令K=GM，则有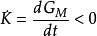：，或。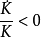

（2）GM值每年的下降值各不相同，即逐年下降值是不均匀的。

**地心引力常数值变化的原因：**地心引力常数值逐年下降的原因是由于万有引力常数和地球质量两者联合变化的结果。

地心引力常数的测定地心引力常数的确定最好是用无线电测距法、激光测量法、多普勒法和射电干涉等方法对已发射的离地球甚远的其它行星的空间探测器在其轨道的被动段测定，这样可以使观测更好地接近二体运动条件。如果利用地球人卫观测方法确定地心引力常数，必须要足够准确地顾及地球引力对卫星轨道的影响，特别是对卫星运动的平均角速度n和轨道长半轴a的影响。

从法方程的制约性来讲，对椭园轨道的探测器是不利的。这时可改变观测量为平均角速度n及轨道长半轴a的办法来达到目的。

在利用激光测月定位技术中，根据万有引力定律可知，两个质点之间是互相吸引的，这就是说，在地-月系统中，不仅地球吸引月球，使月球具有加速度a，同时月球也吸引地球，使地球具有加速度A。设地球质量M，月球质量m，由牛顿第二定律知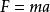，所以月球加速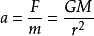，同理，地球加速度。

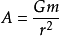由于地球和月球各自受力方向相反，它们的加速度方向也相反，所以在相对运动中，月球相对地球的加速度：；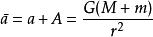

又因作圆周运动的物体的向心加速度a=v2/r，将v=2πr/T代入，得；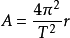

于是得行星运行周期同半径的关系：；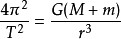

月球平均角速度n月=2π/T，由此可得地心引力常数计算公式：；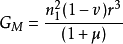

式中ν为太阳等扰动影响改正项，μ=m/M为月球质量同地球质量比，r为月球轨道长半轴。

这是根据激光测月原理来确定地心引力数的基本公式。根据激光测月和其他研究资料的处理和分析，还可以大大地改进月球运动理论，更精确地确定μ值，并更可靠地确定月球激光反射器的月面位置。虽然这种方法将受比例误差的影响，但一般认为用这种方法确定的地心引力常数有较高的内部符合性。1