[科普中国]-物质平衡法

基本原理

将油藏看成体积不变的容器。油藏开发某一时刻，采出的流体量加上地下剩余的储存量，等于流体的原始储量。这里所研究的是流体间的体积平衡，所以也可以说，对于任何一种驱动类型的油藏，在开发过程的任意时刻，油、自由气和水这三者体积变化的代数和为0。1

基本假定对于一个统一水动力学系统的油藏，在建立物质平衡方程式时，应当遵循下列基本假定：

1）油藏的储层物性和流体物性是均质的，各向同性的；

2）相同时间内油藏各点的地层压力都处于平衡状态，并是相等和一致的；

3）在整个开发过程中，油藏保持热动力学平衡，即地层温度保持为常数；

4）不考虑油藏内毛管力和重力的影响；

5）油藏各部位的采出量保持均衡，且不考虑可能发生的储层压实作用。

实际油藏的简化基于以上假设，把一个实际的油藏，简化为封闭的或不封闭的（具有天然水侵）储存油、气的地下容器；

在这个容器内，随着油藏的开采，油、气、水的体积变化服从物质守恒原理，由此原理所建立的方程式称为物质平衡方程式。物质平衡方程式的主要功能是：

1、确定油藏的原始地质储量；

2、判断油藏的驱动机理；

3、测算油藏天然水侵量的大小；

4、在给定产量的条件下预测油藏未来的压力动态。

在建立和应用物质平衡方程式时应注意：特点是地下平衡、累积平衡、体积平衡；在应用物质平衡方程式时，需要注意取全取准地层压力、产量和PV取样分析资料。

应用天然水侵量的计算。

很多油藏的边界常局部或全部地受含水层包围, 这些含水层称为供水区, 而水侵量的变化情况又与供水区的供给能力有关, 天然水侵量的大小主要取决于供水区域的大小、水域的几何形状、油水粘度比、供水区中岩石和水的压缩性、水区与油区的连通性以及两者的压差大小。水侵量的计算与物质平衡方程无关, 它满足自己独立的渗流方程。反过来讲, 只有在确定了水侵规律以后, 才能应用物质平衡方程解决问题。所以, 物质平衡方程式和水侵量计算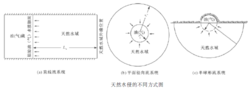是两个必须同时考虑的问题。

建立水侵渗流方程的两个基本假设是:

(1 ) 油气藏作为一口扩大井在供水区中生产;

(2 ) 油气藏连续的地层压力降可用压力梯级来表示。

水侵量计算采用的表达式包括稳定流法和非稳定流法两类。就其天然水侵的几何形状,又可分为直线流、平面径向流和半球形流三种方式( 如图)。

一、稳定流法

1. 稳定状态公式(Schilthuis 模型)

描述水侵特征的最简单方法是Schilthuis 方法。因为它的计算量比其他方法少得多。

在Schilthuis 模型中包含了许多假设:

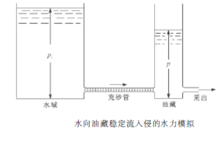
假设供水区非常大并且高渗透, 供水区内总保持着原始压力pi 。图为Schilthuis 模型水力模拟示意图, 在水罐中, 压力面是平的并且保持在pi 不变, 这种情况相当于有地面水补充的自流系统, 或与含油区相比供水区十分大的情况。

Schilthuis 模型的基本方程是表示稳定流关系的达西定律的积分式。若水域中的压力是不变的, 但油藏压力则随着生产而下降, 这就使跨过油水界面的压差越来越大, 这样从水域到油藏的流量实际上不是稳定状态的, 但可处理成一系列“ 稳定状态”。

基于达西稳定流定律, 得到:

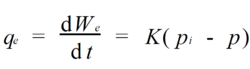
式中:

We———天然累积水侵量( m3 ) ;

pi ———原始地层压力(MPa ) ;

p———某时间t 时的地层压力(MPa) ;

t———开采时间( d) ;

K———水侵常数[m3/ (MPa·d) ] ;

qe———水侵速度( m3 / d)。

二、修正稳定状态公式( Hurst 模型)

天然水驱油藏的开采实际动态表明, 上式中的K并不是一个常数, 而是一个随时间变化的变量。赫斯特( Hur st ) 考虑到天然水域作用范围逐渐扩大的影响, 于1943 年对Schilth uis 公式进行了如下修正:

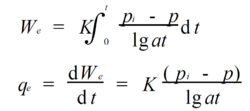
式中: a———与时间单位有关的换算常数。

上式区别在于积分符号内引入了一个时间的对数函数。它的使用条件是, 与含油区相比, 供水区很大; 油层产生的压力降不断向外传播, 使流动阻力增大, 因而边水侵入速度减小。另外, 这一规律一般用于油田生产一段时间以后, 压力处于平稳下降的阶段。2