[科普中国]-三角高程测量

原理

如图1所示，已知点A的高程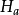 ，B为待定点，待求高程为 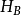。在点A安置经纬仪，照准点B目标顶端M，测得竖直角α。量取仪器高i和目标高v。如果测得AM之间距离为D'，则A、B点的高差 为

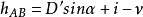如果测得A、B点的水平距离D，则高差 为

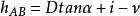
则B点高程为

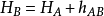
上述计算公式是假定地球表面为水平面(即水准面为水平面)、观测视线为直线的基础上推导而得到的。当地面上两点间距离小于300 m时，可以近似认为这些假设条件是成立的，上述公式也可以直接应用。但两点问的距离超过300 m时，就要考虑地球曲率对高程的影响，加以曲率改正，称为球差改正，其改正数为c。同时，观测视线受大气折光的影响而称为一条向上凸起的弧线，需加以大气折光影响的改正，称为气差改正，其改正数为γ。以上两项改正合称为球气差改正，简称两差改正，其改正数为f=C-γ。

球差改正与气差改正之和可表示为

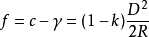
式中：f简称两差改正。因k值大约在0.08～0.14之间，所以，f恒大于零。大气垂直折光系数k是随地区、气候、季节、地面覆盖物和视线超出地面高度等条件的不同而变化的，一般取k=0.14计算两差改正f。

为了减少两差改正数f，《城市测量规范》规定，代替四等水准的光电测距三角高程，其边长不应大于1 km。减少两差改正误差的另一个方法是，在A，B两点同时进行对向观测，此时可以认为k值是相同的，两差改正f也相等。取往返测高差的平均值为

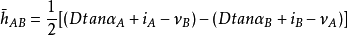可以抵消掉f。1

测量方法(1)在测站上安置仪器（经纬仪或全站仪），量取仪高；在目标点上安置觇标（标杆或棱镜），量取觇标高。

(2)采用经纬仪或全站仪采用测回法观测竖直角口，取平均值为最后计算取值。

(3)采用全站仪或测距仪测量两点之间的水平距离或斜距。

(4)采用对向观测，即仪器与目标杆位置互换，按前述步骤进行观测。

(5)应用推导出的公式计算出高差及由已知点高程计算未知点高程。2

主要误差观测边长D、垂直角a、仪器高i和觇标高口的测量误差及大气垂直折光系数K的测定误差均会给三角高程测量成果带来误差。下面简要介绍之。

(一)边长误差

边长误差决定于距离丈量方法。用普通视距法测定距离，精度只有1/300，就是说，300m的边长，其误差达±1 m；用正弦定理根据三角形内角解析边长，主要决定于角度测量精度，一级小三角的测角中误差为±10''，最弱边边长误差为1/0 000；用电磁波测距仪测距。精度很高，边长误差一般为几万分之一到几十万分之一。边长误差对三角高程的影响与垂直角大小有关，垂直角愈大，其影响也愈大。

(二)垂直角误差

垂直角观测误差包括仪器误差、观测误差和外界环境的影响。仪器误差由经纬仪等级所决定，垂直度盘的分划误差、偏心误差等都是影响因素。观测误差有照准误差、指标水准管居中误差等。外界条件主要是大气垂直折光的影响。J6纬仪两测回垂直角平均值的中误差可达±15''，对三角高程的影响与边长及推算高程路线总长有关，边长或总长愈长，对高程的影响也愈大。因此，垂直角的观测应选择大气折光影响较小的阴天和每天的中午观测较好，推算三角高程路线还应选择短边传递，对路线上的边数也有限制。

(三)大气垂直折光误差

大气垂直折光误差主要表现为折光系数K值的测定误差。实验证明，K值中误差约为±0.03～±0.05。另外，一般采用K的平均值计算球气差γ时，也会有误差。不过，取直、反觇高差的平均值作为高差成果，可以大大减弱大气垂直折光误差的影响。

(四)丈量仪器高和觇标高的误差

仪器高和觇标高的量测误差有多大，对高差的影响也会有多大。因此，应仔细量测仪器高和觇标高。3