[科普中国]-黄海平均海水面

平均海水面

平均海面是指某地一定时期内每小时海面高度的算术平均值，又称平均海水面。它是大地测量和海道测量中的高程起算面，又称零面或基准面。

某地平均海面高度一般从该地验潮站零点（水尺零点）起算。按连续验潮时间长短可分为：日平均海面，即一天24或25个整点时的海面高度的算术平均值。在一天内基本上消除了潮汐影响。月平均海面，连续一个月内的每小时海面高度的算术平均值，基本上消除了每日海面升降的影响。年平均海面，一年内各月的月平均海面高度的算术平均值，基本上消除了气象周期波动的影响,即月平均海面的季节变化。多年平均海面,各年的年平均海面高度的算术平均值，消除了潮汐的长周期（如天文要素以18.6年为周期）波动的影响。多年平均海面一般可用18.6年或更长时期的连续观测资料算得较精确值，也可按各分潮的不同时间的潮高来计算。

平均海面的变化同天文、气象、海水密度、基本环流结构以及地理条件等的影响有密切关系。在同一地点，日平均海面受气象变化，主要是气压和风的变化影响较大。中国的月平均海面有明显的季节变化（主要是海水密度变化和气压变化引起的），而年平均海面差异较小。中国渤海、黄海、东海、南海的各长期验潮站的多年平均海面，相差几厘米至几十厘米。

黄海平均海水面简介解放前，我国没有系统的水准测量，高程基准面极为棍乱地物的高程，北方以大沽零点，东南沿海以吴淞零点，南方则以珠江零点为高程零点。

解放后，为了建立全国统一的高程系统，测绘部门曾经用过坎门验潮站观测的平均海面与青岛验潮站1952~1953年观测的平均海面起算当时的水准成果，并命名为“1954年黄海平均海水面”。1957年又以青岛验潮站1950~1956年七年观测的平均海面作为基准面，并命名“黄海平均海水面”，后又叫“1957年黄海平均海面”。1

理想的高程基准面是大地水准面，但通常用接近于大地水准面的平均海面作为高程基准面。对平均海面的要求:观测地点必须自由通海且不受内河影响，地壳稳定且能避风浪，有水准联测线路且对海区有代表作用，有长期水位观测资料且尽可能满足潮汐周期。1957年，国家根据当时的资料条件，决定采用青岛1950-1956年七年观测的水位资料计算的平均海面，作为我国的统一高程基准面，经过二十多年的努力，我国已经从混乱的高程系统，过渡到以黄海平均海水面为统一高程基准面的高程系统。

存在问题作为我国统一高程基准面，除要求由长期观测资料进行计算，以求得准确的结果外，更重要的是要求它能够符合于当地的实际海面。

“黄海平均海水面”符合于黄海当地的平均海面，更确切地说，还只是符合于青岛大港码头验潮井当地的平均海面。离开青岛验潮站，实际的平均海面就有差异。究竟青岛验潮站这个点所代表的面有多大范围，这是需要根据使用的目的与实际海面的差异而定。我国海区纵贯南北达数千公里，北方的渤海和北黄海，南方的东海和南海，其平均海面与黄海平均海水面差异怎样，这是确定统一高程基准面时需要考虑的另一个问题。

我国沿海各验潮站当地平均海面高于黄海平均海水面，其高度:渤海一般为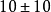 厘米；东海一般为 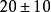厘米；南海一般为 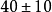厘米。由此看出，我国的平均海面离青岛越远，高于黄海平均海水面的数值越大，最大可达72厘米。平均海面的高度差，每百公里约2厘米。

不管什么原因造成当地平均海面与黄海平均海水面的差异，这个矛盾对于沿海建设和海岸工程带来突出的问题，有些根据统一高程基准面起算有高程值的地物，却长期处于实际的海面下，沿海以当地平均海面起算的与以黄海平均海水面起算的高程系统的归化，由于记载和领会的不一致，还可能造成事故。2

校正高程测量一般可分为四种，即水准测量、三角高程测量、气压高程测量和利用人造地球卫星进行三维定位粗略算出高程。四种方法中以水准测量精度最高。海洋站潮高基准面与国家基本水准点之间的高程差，规范要求定期进行三等水准测量，这种测量两次差值一般不超过1厘米（地震前后测量结果例外）。沿海与大陆直接相连的有潮汐观测的海洋站，这个要求基本上都达到了。海洋站的波浪和气象观测，要求测点高程准确到0.1米，这个要求尽管较低，但在一些无法用水准测量法与大陆联测的海岛站或测点处于离国家水准点较远的岬角，也还不易达到。

许永伦关于测量提出了几点建议：

1，两站距离小于或等于150公里，不管潮汐性质是否相同，较准确的水准测云资料证明，同步月平均海水面之差不超过5厘米。据此，如果甲站的水尺零点经水准测量是准确的，而且与黄海零面的关系也是明确的话，则可假定乙站同步月平均海水面与甲站相同，从而求出乙站水尺零点的高程（误差小于5厘米），还可校正与乙站水尺零点联测的水准点高程。

2，两站距离超过150公里，在一般情况下，要用甲站的月平均海水面确定乙站测点的拔海高程，容易引起0.1米或更大的误差。3