[科普中国]-单位权

权

在科学研究或高准确度测量中，往往在不同的测量条件下，用不同的仪器，不同的测量方法，不同的测量次数以及不同的测量者进行测量与对比，这种测量称为不等精度测量。由于不等精度测量各个测量结果的不可靠程度不一样，因而不能简单地取各测量值的算术平均值作为最后测量结果；而应让可靠程度大的测量结果占的比重大一些，可靠程度小的占比重小一些；这种可靠程度大小的数值表示就是该结果的“权”。

不同精度观测值的可靠性不同，它们在计算最或是值时发挥的影响也应不同。这就需要选定一个比较各观测值之间可靠程度的量，这个量就是“权”。可靠性较大的观测值应具有较大的权。例如，对某一未知量分别进行了两组观测，每组内各个观测值是等精度的。1

单位权简介在等精度测量中，具有同一方差的单次测得值的权数为1，将等于1的权特称为单位权。

在非等精度测量中，由于各测量数据对最终结果的贡献不同，故在数据处理中引入权的概念，即用权的大小来表示某数据与其它数据相比对最终结果贡献的大小。权的大小是相对的，可以根据实际情况来确定。从最小二乘原理来看，权与测量方差成反比，因此为求得非等精度测量下的方差，一般是通过单位权化来实现的。

设对某量进行n次测量，测量值为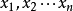，对应的方差为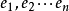，设某数据的权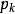= 1，则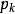称为单位权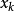，的标准差称为单位权标准差。22

单位权标准差加权的目的是为了权衡非等精度测量数据对最终结果贡献的大小，权的大小是相对的，而加权的对象是各个非等精度测量的数据，加权的原因是由于非等精度测量数据精度不同因而不便利用算术平均去综合得到最终结果。为此，采用单位权化方法对每一非等精度结果加权得：

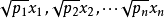
对测量结果乘以各自权的平方根，确已达到单位权化的目的；这说明尽管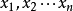是不等精度的测量数据，但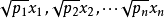却已成为等精度测量的结果，按独立的次等精度测量的数据处理，这时单位权标准差的最佳估计量是：

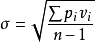
其中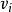为残差。