[科普中国]-真近点角

真近点角简介

真近点角指天体从近地点起沿轨道运动时其向径扫过的角度，（一般用v表示）是某一时刻轨道近地点到卫星位置矢量R的夹角。真近点决定了卫星在轨道中的具体位置。

天体问题共有三种近点角，包括偏近点角、平近点角和真近点角。

偏近点角是过椭圆上的任意一点，垂直于椭圆半长轴，交半长轴外接圆的点到原点的直线与半长轴所成夹角。

平近点角在轨道力学中是轨道上的物体在辅助圆上相对于中心点的运行角度，在测量上不同于其他的近点角，平近点角与时间的关系是线性的。因为与时间是线性的关系，因此要计算在轨道上两点之间移动所需的时间是非常容易的。

三种近点角的关系如图所示，O为椭圆的一个焦点（地球质心），S为卫星在轨道上的位置，r为卫星向径，N为升交点，f为真近

点角，P为近地点。以椭圆中心为圆心，椭圆长半径a为半径的辅助圆，且过S作x轴的垂线交于H，延长SH交辅助圆于S，连接S'，E为x轴与O'S‘夹角，即偏近点角。2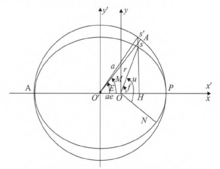

由图可知向径r的坐标为：

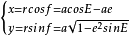
式中，e为椭圆轨道的第一偏心率。

可得由偏近点角E计算真近点角f的公式为：

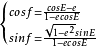
又可解得由真近点角f计算偏近点角E的公式为：

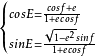
平近点角M与偏近点角E之间的几何关系则由开普勒方程所决定：

研究现状我国卫星已进入快速发展阶段，取得了举世瞩目的成就。卫星的运动虽然比较复杂，但其基础是二体问题。二体问题中引入了各种不同的近点角（平近点角、偏近点角、真近点角）的定义，在卫星星历计算、航天器轨道确定时，经常遇到它们之间的变换问题。偏近点角和平近点角之间的变换即经典的Kepler方程解算是解决这一问题的关键。总的来看，Kepler方程的解法主要有迭代法和直接法两种。随着空间技术和计算机技术在卫星星历计算中的应用和发展，研究各近点角之间的关系具有更加重要的实用价值。对于这一问题，国内外许多学者进行了深人研究。顾晓勤对真近点角超越方程，用级数展开方法直接得到迭代算法，求出真近点角与时间的关系。Peter给出了基于Bessel函数的Kepler方程级数解法，Jan给出了Kepler方程直接解的四元素表示。

高端阳等对近点角间的差异进行了研究，推导出近点角间的差异极值点及其对应极值的表达式，并将其表示为关于偏心率e的幂级数形式。最后以偏心率e=0.01、e=0.1或e=0.2为例，对它们进行了数值分析和对比，得出结论：

（1）近点角间的差异存在极值情况，且极大值与极小值的绝对值相等。

（2）近点角间的差异极值的绝对值跟偏心率e的大小有关，随着偏心率e的增大，近点角间的差异极值的绝对值也随着增大。

（3）将近点角间差异极值点及对应极值表示为符号形式，并统一展开为偏心率e的幂级数形式，该表达式易于比较分析，一定程度上丰富了卫星运动分析理论。3

椭圆轨道真近点角的级数计算在航天器Kepler轨道运动中，一般情况下时间积分不能导出解析形式的原函数。为求椭圆轨道运动周期，引入偏近点角，由变量替代得到以时间为自变量的偏近点角函数超越方程.在确定航天器任意时刻位置时，往往借助于计算机数值模拟计算。有文献讨论了航天器小偏心率椭圆轨道运动。顾晓勤等用级数展开方法直接得到真近点角超越方程，由迭代法求真近点角与时间的关系，讨论迭代收敛的充分条件，对小偏心率椭圆轨道列写真近点角近似方程并求解对于不满足迭代收敛充分条件情形。还列写了偏近点角超越方程，用迭代法求出偏近点角，由数值积分方法求出真近点角与时间的关系，指出所有椭圆轨道都满足偏近点角迭代收敛的充分条件，数值模拟结果表明该方法的有效性。4