矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义1。一般单指矩阵乘积时,指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起,所以有时候可以简便地表示一些复杂的模型,如电力系统网络模型。2
定义设A为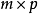 的矩阵,B为
的矩阵,B为 的矩阵,那么称
的矩阵,那么称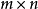 的矩阵C为矩阵A与B的乘积,记作
的矩阵C为矩阵A与B的乘积,记作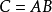 ,其中矩阵C中的第
,其中矩阵C中的第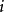 行第
行第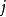 列元素可以表示为:1
列元素可以表示为:1
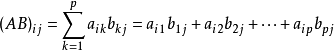
如下所示:

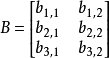
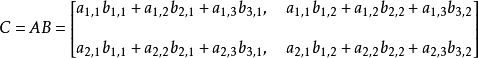
注意事项1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
基本性质乘法结合律: (AB)C=A(BC).3
乘法左分配律:(A+B)C=AC+BC3
乘法右分配律:C(A+B)=CA+CB3
对数乘的结合性k(AB)=(kA)B=A(kB).
转置 (AB)T=BTAT.
矩阵乘法一般不满足交换律4。
其他的乘积形式除了上述的矩阵乘法以外,还有其他一些特殊的“乘积”形式被定义在矩阵上,值得注意的是,当提及“矩阵相乘”或者“矩阵乘法”的时候,并不是指代这些特殊的乘积形式,而是定义中所描述的矩阵乘法。在描述这些特殊乘积时,使用这些运算的专用名称和符号来避免表述歧义。
哈达马积(Hadamard product)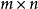 矩阵
矩阵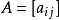 与
与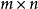 矩阵
矩阵 的Hadamard积记作
的Hadamard积记作 。其元素定义为两个矩阵对应元素的乘积
。其元素定义为两个矩阵对应元素的乘积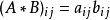 的m×n矩阵3。例如,
的m×n矩阵3。例如,
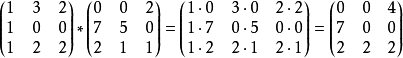
克罗内克积(Kronecker Product)克罗内克积是两个任意大小的矩阵间的运算,符号记作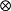 。克罗内克积也被称为直积或张量积.以德国数学家利奥波德·克罗内克命名5。计算过程如下例所示:
。克罗内克积也被称为直积或张量积.以德国数学家利奥波德·克罗内克命名5。计算过程如下例所示:
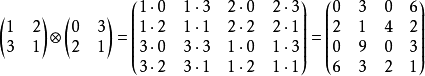
实现C++代码6
struct Matrix:vector//使用标准容器vector做基类,需#include语句{ Matrix(int x=0,int y=0,int z=0)//初始化,默认为0行0列空矩阵 { assign(x,vector(y,z)); } int h_size()const//常量说明不可省,否则编译无法通过 { return size(); } int l_size()const { return empty()?0:front().size();//列数要考虑空矩阵的情况 } Matrix pow(int k);//矩阵的k次幂,用快速幂实现,k为0时返回此矩阵的单位矩阵};Matrix operator*(const Matrix &m,const Matrix &n)//常量引用避免拷贝{ if(m.l_size()!=n.h_size())return Matrix();//非法运算返回空矩阵 Matrix ans(m.h_size(),n.l_size()); for(int i=0; i!=ans.h_size(); ++i) for(int j=0; j!=ans.l_size(); ++j) for(int k=0; k!=m.l_size(); ++k) ans[i][j]+=m[i][k]*n[k][j]; return ans;}Matrix Matrix::pow(int k){ if(k==0) { Matrix ans(h_size(),h_size()); for(int i=0; i!=ans.h_size(); ++i) ans[i][i]=1; return ans; } if(k==2)return (*this)*(*this); if(k%2)return pow(k-1)*(*this); return pow(k/2).pow(2);}实际应用数据统计某公司有四个工厂,分布在不同地区,同时三种产品,产量(单位;t),试用矩阵统计这些数据4。
|| ||
可用下述矩阵描述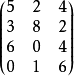 ,其中四行分别表示甲乙丙丁四个工厂的生产情况,三列分布表示三种产品P1,P2,P3的产量。
,其中四行分别表示甲乙丙丁四个工厂的生产情况,三列分布表示三种产品P1,P2,P3的产量。
再设矩阵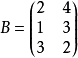 ,其中第一列表示三种产品的单件利润,第二列表示三种产品的单件体积。
,其中第一列表示三种产品的单件利润,第二列表示三种产品的单件体积。
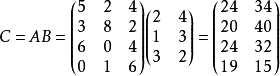
矩阵C的第一列数据分别表示四个工厂的利润,第二列分别表示四个工厂产品需要的存储空间。
路径问题给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数。
把给定的图转为邻接矩阵,即A(i,j)=1当且仅当存在一条边i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),实际上就等于从点i到点j恰好经过2条边的路径数(枚举k为中转点)。类似地,C*A的第i行第j列就表示从i到j经过3条边的路径数。同理,如果要求经过k步的路径数,我们只需要二分求出A^k即可。7
本词条内容贡献者为:
齐臣杰 - 研究员 - 北京信息科技大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国