[科普中国]-双曲线的标准方程

双曲线(Hyperbola)是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹，也可以定义为到定点与定直线的距离之比是一个大于1的常数的点之轨迹1。双曲线是圆锥曲线的一种，即圆锥面与平行于中轴的平面的交截线。

设双曲线的焦距为2c，双曲线上任意一点到焦点F1，F2的距离的差的绝对值等于常数2a(c>a>0)2

以F1，F2所在直线为x轴，线段F1F2的垂直平分线为y轴，建立直角坐标系xOy，则F1，F2的坐标分别为（-c,0），（c,0）

设M（x,y）为双曲线上任意一点，根据双曲线定义知

|MF1-MF2|=2a

即| |=2a

化简得

因为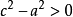

所以令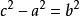 (b>0)得3：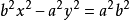

两边除以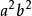 得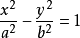 (a>0,b>0即焦点在x轴上)

类似可以得到焦点为F1（0,-c），F2（0,c）的双曲线的方程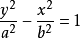 (a>0,b>0即焦点在y轴上)

以上两种方程都叫做双曲线的标准方程4。

本词条内容贡献者为:

杨磊 - 副教授 - 北京大学数学学院