[科普中国]-自由沉降比

概念

矿物颗粒重选可概括为松散—分层和搬运—分离过程。置于分选设备内的散体物料，在运动介质中，受到流体浮力、动力或其它机械力的推动而松散，被松散的矿粒群，由于沉降时运动状态的差异，不同密度（或粒度）颗粒发生分层转移。按重选来讲，就是要达到按密度分层，通过运动介质的作用达到分离。其基本规律可概括为：松散—分层—分离。重选理论研究的问题，简单来说就是探讨松散与分层的关系。松散和搬运分离几乎都是同时发生的。但松散是分层的条件，分层是目的，而分离则是结果。其工作原理主要受到以下四条基本原理的支配：

（1）颗粒及颗粒群的沉降理论；

（2）颗粒群按密度分层的理论；

（3）颗粒群在回流转中分层的理论；

（4）颗粒群在斜面流中的分选理论。

以上有关颗粒及颗粒群的沉降理论，主要是研究颗粒沉降规律的。1颗粒在介质中的沉降可以分为两种形式，即自由沉降与干涉沉降。严格来说，单个矿粒在无限宽阔的介质(水、空气、重液 )空间内的沉降才是真正的自由沉降。这时矿粒只受到介质的阻力，而不受任何机械阻力的作用。这种情况实际上是不存在的，在重选理论研究中，一般是将矿粒在固体容积浓度小于3%的介质中沉降，是自由沉降的。因为当矿浆浓度很稀时，矿粒在其中沉降所受周围矿粒和器壁对其直接和间接的干涉（即机械阻力)很小，可以忽略不计。因此可以近似地认为是自由沉降。当矿浆浓度增大后，矿粒受到周围矿粒直接摩擦和碰撞，以及它们之间间接通过介而来的介质阻力干涉增大，并且浓度越大，机械阻力越大，干涉作用越强，这种矿粒群在有限容器的沉降运动，叫做干涉沉降。在生产实践中，大多数情况属于干涉沉降。矿粒在干涉沉降时，由于所受的阻力较大，所以与自由沉降相比，其沉降速度较慢。自由沉降比即单个颗粒在流体中沉降，或者颗粒群在流体中分散得较好而颗粒在互不接触、互不干扰得条件下沉降，颗粒的直径比。2

公式两等沉颗粒，其直径和密度分别以dv1、δ1及dv2、δ2表示，且设δ2>δ1,因v1=v2,颗粒等沉，所以dv1>dv2，故等沉比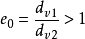

自由沉降比的大小，可由沉降末速的个别公式或通式写出：

如两颗粒等沉，则v1=v2，那么按通式可求得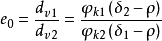

由于等沉比通式中包含阻力系数φ，在非自由沉降的前提条件下，无法直接计算，所以e0常借助个别公式来求得。但两个等沉比颗粒必须在同一性质阻力范围内。对于形状不规则得矿数还应把球形系数x考虑在内。这些公式包括：

(1)按斯托克斯公式求e0，对形状不规则得矿粒，当v1=v2时，即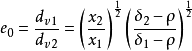

(2)按阿连公式求e0，同理得

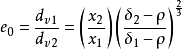(3)按牛顿—雷廷智公式求e0，同理得

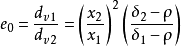将球形因素考虑在内，通常将公式简化为 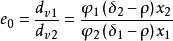3

e0的大小在一定程度上反映了两个等沉颗粒密度差异的大小；同一矿石中不同密度矿粒的e0越大，越易分选。同时e0大小也随介质密度ρ的增大而增大，且e0还是阻力系数φ的函数。理论和实践均表明，e0将随矿粒粒度变细而减小，e0越大，意味着可选的粒级范围越宽。1

影响因素重力沉降过程中，最常见的介质运动形式有静止、上升和下降流动三种。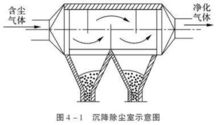单个颗粒在无限宽广的介质中的沉降，称为自由沉降，这是最简单的沉降运动形式。其中运动状态受重力和阻力支配。矿粒在介质中所受重力（G0）等于它在真空中的重力（G）与浮力（F）之差，即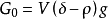

由于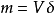

故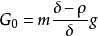

式中 V——矿粒的体积，m3；

δ——矿粒的密度，kg/m3；

ρ——介质的密度，kg/m3；

g——重力加速度，m/g2；

m——矿粒的质量，kg。

可见，矿粒在介质中的重力与矿粒的尺寸、密度及介质的密度有关。自由沉降比随密度的增加而增加。4

阻力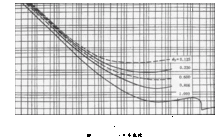矿粒在介质中运动时，由于介质质点间内聚力的作用，最终表现为阻滞矿粒运动的作用力，这种作用力叫介质阻力。介质阻力始终与矿粒相对于介质的运动速度方向相反。由于介质的惯性，使运动矿粒前后介质的流动状态和动压力不同，这种压力差所引起的阻力，称为压差阻力。由于介质的粘性，使介质分子与矿粒表面存在粘性摩擦力，这种因粘性摩擦力所致的阻力，称为摩擦阻力。介质阻力由压差阻力和摩擦阻力所组成，这两种阻力同时作用在矿粒上。介质阻力的形式与流体的绕流流态即雷诺数Re有关。不同情况下，它们各自所占比例不同，但归根结底，都由介质粘性所知。因此矿物在介质中的自由沉降比不是常数，因形状、沉降速度、阻力系数等而变。5

研究意义研究等降现象与自由沉降比的实际意义，目的是为了结合重力分选过程。

(1)当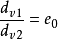 ,表明v1=v2，末速相等，两颗粒自由沉降；

(2)当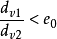 ,表明v1v2，轻矿物颗粒的沉降末速大于重矿物颗粒的沉降末速，按粒度分层，说明密度不同的两种矿粒粒度差大，称为“宽级别”。3