[科普中国]-Bellman-Ford算法

贝尔曼-福特算法（英语：Bellman–Ford algorithm），求解单源最短路径问题的一种算法，由理查德·贝尔曼（Richard Bellman） 和 莱斯特·福特 创立的。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行次松弛操作，得到所有可能的最短路径。其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达。但算法可以进行若干种优化，提高了效率。

介绍Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权，在没有负权回路（回路的权值和为负，即便有负权的边）存在时，也可以采用Bellman - Ford算法正确求出最短路径。

Bellman-Ford算法能在更普遍的情况下（存在负权边）解决单源点最短路径问题。对于给定的带权（有向或无向）图 G=(V,E), 其源点为s，加权函数 w是 边集 E 的映射。对图G运行Bellman - Ford算法的结果是一个布尔值，表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路，算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。

算法贝尔曼-福特算法与迪科斯彻算法类似，都以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解。在两个算法中，计算时每个边之间的估计距离值都比真实值大，并且被新找到路径的最小长度替代。 然而，迪科斯彻算法以贪心法选取未被处理的具有最小权值的节点，然后对其的出边进行松弛操作；而贝尔曼-福特算法简单地对所有边进行松弛操作，共 |V|-1次，其中 |V|是图的点的数量。在重复地计算中，已计算得到正确的距离的边的数量不断增加，直到所有边都计算得到了正确的路径。这样的策略使得贝尔曼-福特算法比迪科斯彻算法适用于更多种类的输入。

贝尔曼-福特算法的最多运行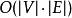 （大O符号）次，|V|和 |E|分别是节点和边的数量）1。

原理松弛每次松弛操作实际上是对相邻节点的访问，第 n次松弛操作保证了所有深度为n的路径最短。由于图的最短路径最长不会经过超过 |V|-1条边，所以可知贝尔曼-福特算法所得为最短路径。

负边权操作与迪科斯彻算法不同的是，迪科斯彻算法的基本操作“拓展”是在深度上寻路，而“松弛”操作则是在广度上寻路，这就确定了贝尔曼-福特算法可以对负边进行操作而不会影响结果。

负权环判定因为负权环可以无限制的降低总花费，所以如果发现第 n次操作仍可降低花销，就一定存在负权环。

优化循环的提前跳出在实际操作中，贝尔曼-福特算法经常会在未达到 |V|-1次前就出解， |V|-1其实是最大值。于是可以在循环中设置判定，在某次循环不再进行松弛时，直接退出循环，进行负权环判定。

队列优化主条目：最短路径快速算法

西南交通大学的段凡丁于1994年提出了用队列来优化的算法。松弛操作必定只会发生在最短路径前导节点松弛成功过的节点上，用一个队列记录松弛过的节点，可以避免了冗余计算。原文中提出该算法的复杂度为O(k|E|)}，k是个比较小的系数，但该结论被证明不适于于所有情况。

Pascal语言示例

1 Begin 2 initialize-single-source(G,s); 3 initialize-queue(Q); 4 enqueue(Q,s); 5 while not empty(Q) do 6 begin 7 u:=dequeue(Q); 8 for each v∈adj[u] do 9 begin10 tmp:=d[v];11 relax(u,v);12 if (tmpd[v]) and (not v in Q) then13 enqueue(Q,v);14 end;15 end;16 End;C++语言示例

int SPFA(int s) { 2 queue q; 3 bool inq[maxn] = {false}; 4 for(int i = 1; i dis[x] + e[i].w) { 13 dis[k] = dis[x] + e[i].w; 14 if(!inq[k]) { 15 inq[k] = true; 16 q.push(k); 17 } 18 } 19 } 20 } 21 for(int i = 1; i