[科普中国]-莱洛三角形

莱洛三角形，也译作勒洛三角形或弧三角形、圆弧三角形，是除了圆形以外，最简单易懂的勒洛多边形，一个定宽曲线1。其作法为先画正三角，然后分别以三个顶点为圆心,边长长为半径画弧所得到的三角形。

做图法弧三角形,又叫莱洛三角形, 是机械学家莱洛首先进行研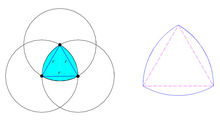究的.弧三角形是这样画的;先画正三角，然后分别以三个顶点为圆心,边长长为半径画弧得到的三角形2。

面积关系通过勒贝格积分可以算出，勒洛三角是定宽曲线所能构成的面积最小的图形，其面积为1/2(π-√3)s²，s为定宽宽度。

性质将一个曲线图放在两条平行线中间，使之与这两平行线相切，则可以做到：无论这个曲线图如何运动，只要它还是在这两条平行线内，就始终与这两条平行线相切，但中心点会形成一个圆。这个定义由Franz Reuleaux,一个十九世纪的德国工程师命名3。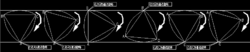

应用1、莱洛三角形也是“除了圆形以外，还有什么形状的下水道盖不会掉入下水道？”这个问题的一个答案。

2、下图为此类三角形旋转的一个例子，因为这个特点，该类三角形可用于做运输的轮子，搬东西稳定（但由于制作技术要求高，边角不耐磨等原因不常用）。

还有一个用圆形而不用莱洛三角做轮子的原因：

用圆作车轮是人类文明发展过程中选择的结果，不仅由于圆的定宽性，还由于圆是最常见的图形之一，比如太阳，月亮等，也是所有定宽曲线中最简单的。圆形较为容易加工。而且定宽的稳定性较好，即使圆形不算正规，还会保持较好的定宽性。

人们将车轮做成圆形，是利用了圆的一个重要性质：将一个圆放在两条平行线中间，使之与这两平行线相切。则可以做到：无论这个圆如何运动，它还是在这两条平行线内，并且始终与这两条平行线相切。此即圆的定宽性质，具有类似圆的定宽性质的曲线称为定宽曲线。

另外，圆形还具有一条重要的性质，几何中心的稳定性，圆的中轴（过圆心的轴）在圆转动的时候是保持高度不变的，始终是地面往上半径的高度。

试想用上面的莱洛三角形，它的几何中心是不稳定的，随着图形的转动上下跳动，这样是不适合做车轮的。

基于上诉特点，圆形的车轮是应用最广泛的。

3、莱洛三角形形状的钻头可钻出四角为圆弧的正方形的孔。4

本词条内容贡献者为:

李健 - 讲师 - 重庆邮电大学