[科普中国]-抛物线方程

抛物线方程是指抛物线的轨迹方程，是一种用方程来表示抛物线的方法1。在几何平面上可以根据抛物线的方程画出抛物线。抛物线在合适的坐标变换下，也可看成二次函数图像。

定义抛物线定义：平面内与一个定点F 和一条直线l 的距离相等的点的轨迹叫做抛物线，点F 叫做抛物线的焦点，直线l 叫做抛物线的准线，定点F不在定直线上。它与椭圆、双曲线的第二定义相仿，仅比值（离心率e）不同，当e=1时为抛物线，当00）

y^2=-2px（p>0）

x^2**=2p****y（p>0）**

x^2**=-2p****y（p>0）**

对于抛物线y^2=2px(p≠0)上的点的坐标可设为(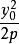,y0)，以简化运算。

抛物线的焦点弦：设过抛物线y^2=2px(p>0)的焦点F的直线与抛物线交于A（x1，y1）、B（x2，y2），直线OA与OB的斜率分别为k1,k2，直线l的倾斜角为α，则有y1y2=-p^2，x1x2=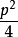，k1k2=-4，|OA|=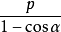,|OB|=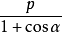,|AB|=x1+x2+p。

几何性质方程的具体表达式为y=ax^2+bx+c

⑴a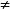0

⑵a>0，则抛物线开口朝上；a0，图象与x轴交于两点：

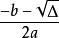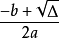（，0）和（，0）；

Δ=0，图象与x轴交于一点：

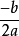（，0）；

Δ0。若抛物线交y轴为负半轴，则c