函数定义域:数学名词,是函数的三要素(定义域、值域、对应法则)之一,对应法则的作用对象。指函数自变量的取值范围,即对于两个存在函数对应关系的非空集合D、M,集合D中的任意一个数,在集合M中都有且仅有一个确定的数与之对应,则集合D称为函数定义域。1
函数设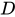 ,
,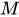 为两个非空实数集,如果按照某个确定的对应法则
为两个非空实数集,如果按照某个确定的对应法则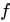 ,使得对于集合
,使得对于集合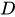 中的任意一个数
中的任意一个数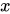 ,在集合
,在集合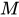 中都有且仅有一个确定的数
中都有且仅有一个确定的数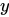 与之对应,那么就称
与之对应,那么就称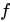 为定义在集合
为定义在集合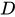 上的一个函数,记做
上的一个函数,记做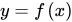 。其中,
。其中,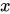 为自变量,
为自变量,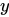 为因变量,
为因变量,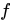 称为对应关系,集合
称为对应关系,集合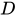 称为函数
称为函数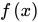 的定义域,
的定义域, 为函数f的值域,对应关系、定义域、值域为函数的三要素。1
为函数f的值域,对应关系、定义域、值域为函数的三要素。1
定义域定义在一个函数关系中,自变量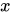 的取值范围
的取值范围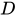 叫作函数的定义域。1
叫作函数的定义域。1
分类函数的定义域是根据函数要解决的问题来定义的,函数的定义域一般有三种定义方法:
(1)自然定义域,若函数的对应关系有解析表达式来表示,则使解析式有意义的自变量的取值范围称为自然定义域。例如函数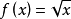 ,要使函数解析式有意义,则
,要使函数解析式有意义,则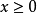 ,因此函数的自然定义域为
,因此函数的自然定义域为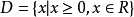 ;
;
(2)函数有具体应用的实际背景。例如,函数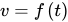 表示速度与时间的关系,为使物理问题有意义,则时间
表示速度与时间的关系,为使物理问题有意义,则时间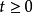 ,因此函数的定义域为
,因此函数的定义域为 ;
;
(3)人为定义的定义域。例如,在研究某个函数时,仅考察函数的自变量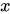 在[0,10]范围内的一段函数关系,因此定义函数的定义域为[0,10]。1
在[0,10]范围内的一段函数关系,因此定义函数的定义域为[0,10]。1
求解方法组合函数由若干个基本函数通过四则运算形成的函数,其定义域为使得每一部分都有意义的公共部分。
原则:(1)分式的分母不能为零;(2)偶次方根的内部必须非负即大于等于零;(3)对数的真数为正,对数的底数大于零且不等于1;(4)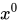 中,
中,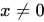 。
。

复合函数若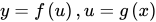 ,则
,则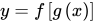 就叫做f和g的复合函数。其中
就叫做f和g的复合函数。其中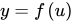 叫做外函数,
叫做外函数,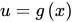 叫做内函数。
叫做内函数。
例如:(1)已知 的定义域
的定义域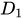 ,求
,求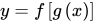 的定义域
的定义域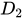 。
。
解法:解不等式:
(2)已知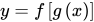 的定义域
的定义域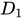 ,求
,求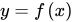 的定义域
的定义域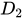 。
。
解法:令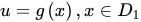 ,求函数
,求函数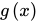 的值域。2
的值域。2
本词条内容贡献者为:
郎奠波 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国