[科普中国]-正方形判定定理

正方形是特殊的平行四边形之一。即有一组邻边相等，并且有一个角是直角的平行四边形称为正方形。正方形判定定理是几何学里用于判定一个四边形是否为正方形的判定定理。判别正方形的一般顺序为先说明它是平行四边形；再说明它是菱形(或矩形)；最后说明它是矩形(或菱形)。

正方形定义：正方形是特殊的平行四边形之一。即有一组邻边相等，并且有一个角是直角的平行四边形称为正方形1。

性质：正方形具有平行四边形、长方形、菱形的一切性质。

①对边平行且相等。

②四条边都相等。

③四个角都是直角。

④两条对角线相等,互相垂直平分,且平分每组对角。

⑤正方形是轴对称图形,也是中心对称图形。

周长：正方形的周长等于它的边长的4倍。若正方形的边长为a，周长为C，那么C=4a。

例:一个正方形的边长为4厘米,求这个正方形的周长。

解：C=4a=4×4=16(厘米)。2

面积：

已知正方形的边长为a，对角线长为d，则正方形的面积 。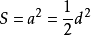

判定定理1、对角线互相垂直平分且相等的四边形是正方形。

2、邻边相等且有一个内角是直角的平行四边形是正方形。

3、有一组邻边相等的矩形是正方形3。

4、有一个内角是直角的菱形是正方形。

5、对角线相等的菱形是正方形。

6、对角线互相垂直的矩形是正方形。

7、有三个内角为直角且有一组邻边相等的四边形是正方形。

判别正方形的一般顺序：先说明它是平行四边形；再说明它是菱形(或矩形)；最后说明它是矩形(或菱形)。

一个角为直角，并且一组邻边相等的平行四边形，叫做正方形。如图3-20的平行四边形ABCD中，∠A为直角，AB=BC，那么平行四边形ABCD就是正方形。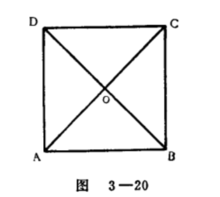

因为正方形是平行四边形，也是矩形，又是菱形，所以它具有平行四边形、矩形、菱形的一切性质4。

相关拓展1、正方形与平行四边形、矩形、菱形的关系：

正方形是特殊的矩形和特殊的菱形，也就是说，正方形既是矩形又是菱形，还是平行四边形，它们的包含关系。如图：

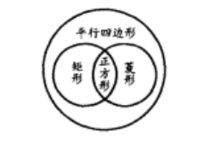
2、正方形的对称性

正方形既是轴对称图形，又是中心对称图形，有四条对称轴对称轴的交点是对称中心，如图所示：

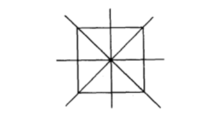
两条对角线所在的直线和两组对边中点所确定的直线都是正方形的对称轴。

3、正方形的两条对角线把正方形分成四个全等的等腰直角三角形，如图：

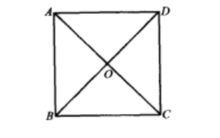
如图，已知四边形ABCD是正方形，对角线AC、BD相交于点O

求证：△ABO、△BOO、△CDO、△DAO是全等的等腰直角三角形

证明：∵四边形ABCD是正方形,

∴AC=BD,AC⊥BD,

AO=BO=CO=DO.

∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,

并且△ABO≌△BCO≌△CDO≌△DAO.

本词条内容贡献者为:

韩彦昌 - 教授 - 华南师范大学数学科学学院