[科普中国]-零状态响应

零状态响应是电路的储能元器件（电容、电感类元件）无初始储能，仅由外部激励作用而产生的响应。零状态响应是系统在无初始储能或称为状态为零的情况下，仅由外加激励源引起的响应。根据叠加原理，将零输入响应与零状态响应两个分量进行叠加，即可得到全响应。1

2

引发原因系统的初始状态为零，仅由激励源引起的响应被称之为该系统的“零状态响应”。

实例：一个原来没有充过电的电容器通过电阻与电源接通，构成充电回路，那么电容器两端的电压或回路中的电流就是系统零状态响应。

本质系统的零状态响应一般分为两部分，它的变化形式分别由系统本身的特性和激励源所决定。当系统是线性的，它的特性可以用线性微分方程表示时，零状态响应的形式是若干个指数函数之和再加上与激励源形式相同的项。前者是对应的齐次微分方程的解，其中指数函数的个数等于微分方程的阶数，也就是系统内部所含“独立”储能元件的个数。后者是非齐次方程的特解。对于实际存在的无源系统而言，零状态响应中的第一部分将随着时间的推移而逐渐地衰减为零，因此往往又把这一部分称之为响应的“暂态分量”或“自由分量”；后者与激励源形式相同的部分则被称之为“稳态分量”或“强制分量”。

全响应系统的全响应是系统或电路在输入和初始条件共同作用下的响应。其可以分成零输入响应和零状态响应两种分量，也可以分成自然响应和受迫响应两种分量，还可以分成瞬态响应和稳态响应两种分量。

求解方法连续线性时不变系统零状态响应的分析方法3：

时域分析1. 时域经典分析法：指利用数学经典理沦，来求解系统微分方程的过程

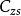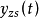步骤：（1）构建系统的时域微分方程；（2）列写特征多项式，求出特征根；（3）求解出方程的齐次解、特解的一般形式；（4）将全解表达式带回原方程，得出待定系数 ，求出 表达式

说明：微分方程的全解由齐次解和特解两部分组成，其中齐次解的形式由微分方程对应的齐次方程的特征根确定，特解由输入激励的形式决定。

时域经典解析法具有下面特点:

（1）优点:思路清晰，便于理解

（2）缺点:用到数学知识，运算量较大，对于复杂输入信号，不易求得特解。

2. 时域卷积法

步骤：（1）构建系统的时域微分方程；（2）求出冲激响应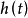 ；（3）计算零状态响应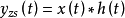

时域卷积法具有下面特点:

（1）优点：适用于复杂输入信号时的零状态响应的分析。

（2）缺点：要计算系统的冲激响应及卷积积分，过程繁琐。

频域(复频域)分析1. 频域分析法

步骤：（1）构建系统的频域电路代数方程；（2）解代数方程，求取系统的频率响应；（3）根据傅里叶变换公式，计算输入信号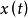 的傅里叶变换式 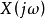；（4）根据傅里叶变换的时域卷积性质有:

综上分析过程，频域分析法特点:

（1）优点:将时域卷积积分转换到频域乘积，或将时域微分方程转换为频域代数方程，简化计算。并引入了频谱函数的概念，对求解冲激响应很有帮助。

（2）缺点:不满足绝对可积条件的信号，其傅里叶变换无意义或不存在。

2. 复频域分析法

为了解决频域分析中的局限性这一问题，将任意连续信号乘上一个衰减因子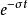使得两者的乘积绝对可积，然后再对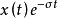进行傅里叶变换。这样傅里叶变换就转换为拉普拉斯变换。

步骤：

方法1：（1）构建系统的复频域代数方程，令输出量及其各阶导数在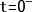时的值为零。(2)对输出量的复频域函数取逆变换，既得系统的零状态响应。

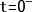方法2：（1）构建系统的复频域代数方程，并令输出量及其各阶导数在时的值为零。(2)求出系统函数

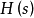，输入信号的拉氏变换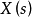。（3）利用拉氏变换卷积性质，求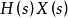的积的拉氏逆变换，既得零状态响应。

复频域分析法的特点：

将时域卷积积分转换到复频域乘积，或将时域微分方程计算转换到复频域代数方程，简化计算，而且也解决了频域分析的局限性问题。

本词条内容贡献者为:

张海霞 - 教授 - 北京大学信息科学技术学院