[科普中国]-KMO检验

KMO（Kaiser-Meyer-Olkin)检验统计量是用于比较变量间简单相关系数和偏相关系数的指标。主要应用于多元统计的因子分析。KMO统计量是取值在0和1之间。

当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时，KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作因子分析；当所有变量间的简单相关系数平方和接近0时，KMO值越接近于0,意味着变量间的相关性越弱，原有变量越不适合作因子分析。

定义KMO检验是 Kaiser, Meyer和 Olkin提出的抽样适合性检验( Measure of Sampling Adequacy)。该检验是对原始变量之间的简相关系数和偏相关系数的相对大小进行检验。1计算公式为：

检验的原理:如果原始数据中确实存在公共因子，则各变量之间的偏相关系数应该很小，这时，KMO的值接近于1，因此，原数据适用于因子分析。

标准Kaiser给出了常用的KMO度量标准: 0.9以上表示非常适合；0.8表示适合；0.7表示一般；0.6表示不太适合；0.5以下表示极不适合。KMO统计量是取值在0和1之间。当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时，KMO值接近1。KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作因子分析；当所有变量间的简单相关系数平方和接近0时，KMO值接近0.KMO值越接近于0,意味着变量间的相关性越弱，原有变量越不适合作因子分析。

|| ||

因子分析的统计检验因子分析已被人们广泛应用于各种数据，但应用的效果相差极大。有的应用效果很好，有的应用效果很差。

因子分析的目的是在互为相关的许多变量中寻找能反映它们之间内在联系以及起主导作用的、数目较少的因子，通过对这些因子的研究,既无损于原来多个变量的信息，又便于对它们进行分类和解释。因此，要想使用因子分析方法，其前提是:原始数据中多个变量之间应有较强的线性相关关系。如果原始变量之间的线性相关程度太小，它们之间就不存在具有说服力的公因子，这时进行因子分析就没有实际意义；如果各个变量之间相互独立，这时多变量的协方差矩阵是对角阵，显然这样的数据是不适合用因子分析进行分析。所以，在应用因子分析时，首先要判断数据是否适宜使用因子分析，也就是要进行因子分析的适用性检验，根据分析可知：因子分析的适用性检验就是假设原始变量之间存在着较强的线性相关，这可以对变量的相关系数矩阵进行检验2。

Bartlett球性检验Bartlett球性检验是一种数学术语。用于检验相关阵中各变量间的相关性，是否为单位阵，即检验各个变量是否各自独立。因子分析前，首先进行KMO检验和巴特利球体检验。在因子分析中，若拒绝原假设，则说明可以做因子分析，若不拒绝原假设，则说明这些变量可能独立提供一些信息，不适合做因子分析。

因子分析前，首先进行KMO检验和巴特利球体检验。KMO检验用于检查变量间的相关性和偏相关性，取值在0~1之间。KMO统计量越接近于1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。实际分析中，KMO统计量在0.7以上时效果比较好；当KMO统计量在0.5以下，此时不适合应用因子分析法，应考虑重新设计变量结构或者采用其他统计分析方法。

反映像相关矩阵的检验反映像相关矩阵检验是通过偏相关系数矩阵进行的检验，反映像相关矩阵中非对角线元素是变量偏相关系数的相反数。如果原始变量中确实存在起作用的公因子，则各变量之间的偏相关系数应该很小,因为它与其他变量重叠的影响因素被扣除掉了，所以，如果反映像相关矩阵中的很多元素值比较大时，说明该原始变量不适合进行因子分析。反映像矩阵中对角线元素是与KMO类似的指标MSA( Measures of SamplingAdequacy)，MSA值计算结果显示在反映像相关矩阵的主对角线上。第i个变量MSA值的计算公式是：

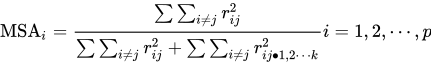
式中：p为自变量个数，其他符号的意思同上。

MSA值的求和项中只包含互不相同的变量之间的相关系数和偏相关系数。即每个变量与其他变量的相关系数和偏相关系数就可以算出一个MSA值，因此共有p个MSA值。因此MSA值可以反映每个变量的抽样合适度，MSA值的使用标准同KMO值一样，越接近1，说明原始变量越适合做因子分析，一般应在0.60以上。3

本词条内容贡献者为:

郎奠波 - 副教授 - 黑龙江财经学院