如果存在一个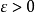 ,使得对于任意满足
,使得对于任意满足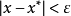 的
的 都有
都有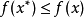 ,我们就把点
,我们就把点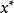 对应的函数值
对应的函数值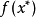 称为函数
称为函数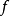 的一个局部最小值。从函数图象上看,局部最小值就像是山谷的底部。
的一个局部最小值。从函数图象上看,局部最小值就像是山谷的底部。
局部最大值:
如果存在一个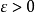 ,使得对于任意满足
,使得对于任意满足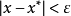 的
的 都有
都有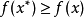 ,我们就把点
,我们就把点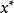 对应的函数值
对应的函数值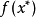 称为函数
称为函数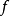 的一个局部最大值。从函数图象上看,局部最小值就像是山谷的顶部。2
的一个局部最大值。从函数图象上看,局部最小值就像是山谷的顶部。2
全局最大值:
如果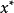 对于任意的
对于任意的 都满足
都满足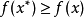 ,则称
,则称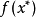 为函数
为函数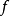 的全局最大值
的全局最大值
全局最小值:
如果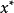 对于任意的
对于任意的 都满足
都满足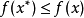 ,则称
,则称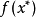 为函数
为函数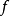 的全局最小值
的全局最小值
设3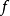 在点
在点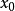 连续,在某邻域
连续,在某邻域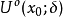 内可导。
内可导。
(1)若当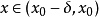 时,
时,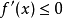 ,当
,当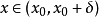 时,
时,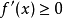 ,则
,则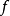 在点
在点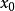 取得极小值。
取得极小值。
(2)若当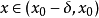 时,
时,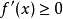 ,当
,当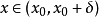 时,
时, ,则
,则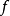 在点
在点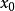 取得极大值。
取得极大值。
设3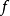 在点
在点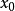 连续,在某邻域
连续,在某邻域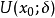 内一阶可导,在
内一阶可导,在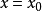 处二阶可导,且
处二阶可导,且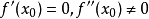 。
。
(1)若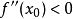 ,则
,则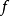 在
在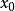 取得极大值
取得极大值
(2)若 ,则
,则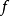 在
在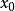 取得极小值
取得极小值
设3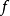 在
在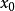 的某邻域内存在知道
的某邻域内存在知道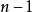 阶导函数,在
阶导函数,在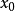 处
处 阶可导,且
阶可导,且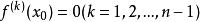 ,
,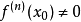 ,则
,则
(1)当 为偶数时,
为偶数时,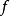 在
在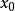 处取得极值,且当
处取得极值,且当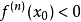 时取得极大值,
时取得极大值, 时取得极小值
时取得极小值
(2)当 为奇数时,
为奇数时,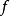 在
在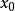 处不取极值
处不取极值
多元函数的极值问题是多元函数微积分的重要应用,这里二元函数为例进行讨论。
定义设函数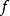 在点
在点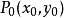 的某邻域
的某邻域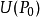 内有定义。若对于任何点
内有定义。若对于任何点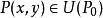 ,成立不等式
,成立不等式
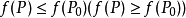 则称函数
则称函数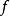 在点
在点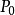 取得极大(极小)值,点
取得极大(极小)值,点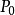 称为
称为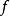 的极大(极小)值点。极大值、极小值统称为极值。极大值点、极小值点统称为极值点。4
的极大(极小)值点。极大值、极小值统称为极值。极大值点、极小值点统称为极值点。4
注意:这里所讨论的极值点只限于定义域的内点
极值必要条件若函数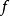 在点
在点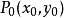 存在偏导数,且在
存在偏导数,且在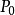 取得极值,则有
取得极值,则有
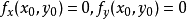 反之,若函数
反之,若函数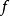 在点
在点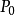 满足上式,则称点
满足上式,则称点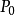 为
为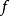 的稳定点。
的稳定点。
设二元函数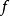 在点
在点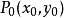 的某邻域
的某邻域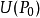 上具有二阶连续偏导数,且
上具有二阶连续偏导数,且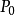 是
是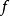 的稳定点。则当
的稳定点。则当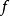 在
在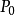 处的黑塞(Hesse)矩阵是正定矩阵时,
处的黑塞(Hesse)矩阵是正定矩阵时,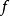 在点
在点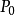 取得极小值;当
取得极小值;当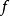 在
在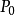 处的黑塞(Hesse)矩阵是负定矩阵时,
处的黑塞(Hesse)矩阵是负定矩阵时,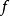 在点
在点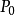 取得极大值;当
取得极大值;当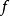 在
在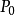 处的黑塞(Hesse)矩阵是不定矩阵时,
处的黑塞(Hesse)矩阵是不定矩阵时,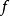 在点
在点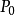 不取极值。
不取极值。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国