[科普中国]-内模控制

简介

1982年，C.E.Garcia和M.Morari提出具有模型、控制、反馈环节的内模控制结构，其产生背景主要有两个方面：一是对当时的两种预测控制算法MAC和DMC进行系统分析；其次是作为Smith预估器的一种扩展，其设计更为简单，鲁棒性及抗干扰性大为改善。

内模控制(Internal Model Control,简称IMC)是一种基于过程数学模型进行控制器设计的新型控制策略。IMC具有实用性强，结构简单，设计直观，不需要精确的对象模型，在线调节参数少，调整容易等优点。特别是对于鲁棒性及抗干扰性的改善和对大时滞系统的控制，效果尤为显著，而且也为非线性系统的控制提供了一条有效的途径。由于具有良好的跟踪性能和抗干扰能力，并对模型失配有一定的鲁棒性，使其在工业过程控制中获得了越来越广泛的应用。

此外，内模控制还和许多其它控制方式相结合，如内模控制与模糊控制、内模控制和自适应控制、内模控制和最优控制、预测控制的结合使内模控制不断得到改进并广泛应用于工程实践中，取得了良好的效果。1

内模控制的基本原理如图1所示的是内模控制的一般结构图，其中，U ( s )为输入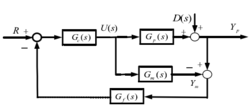变量，R为设定值，D ( s )为外部干扰项Yp、Ym分别为对象输出和内部模型输出；Gp(s)为被控对象；Gm(s)为内部模型；Gc(s)为内模控制器；Gf(s)为反馈滤波器。

根据图1，可以表示出内模控制器的闭环输出为(式1)：

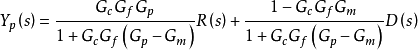
当Gf=1时，该系统为1自由度系统，可以通过调节控制器Gc来改善系统的动态伺服特性、抗干扰性和鲁棒性能；当Gf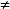 1时，该系统变为2自由度系统，反馈滤波器Gf的存在可以帮助调节系统动态响应特性和稳态特性间的平衡，综合提高被控系统的控制品质。2

内模控制的基本性质当系统为1自由度系统，即Gf=1时，内模控制器有以下三个基本性质：对偶稳定性、理想控制器特性和零稳态偏差特性。

内模控制的对偶稳定性在 Gp(s)= Gm(s)，即模型精确匹配时，图1所示的可等效为开环结构，意味着只要满足稳定条件，即控制器以及对象都是稳定的，那么有系统是闭环稳定的，这就客观上保证了内模控制系统的稳定性。对偶稳定性的重大意义在于简化了系统稳定性的分析，特别是对于复杂的大滞后对象、非线性对象的研究，可以极大程度减少运算，提高控制系统设计的整体效率。

内模控制的理想控制特性不妨设 Gp(s)= Gm(s)，且Gp(s)稳定，若存在内模控制器Gc(s)=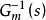 ，且对象模型的逆物理可实现时，无论外界干扰D ( s )是否为0，都有输出Y ( s ) =R ( s)，说明 IMC 可消除干扰，实现理想控制。

内模控制的零稳态偏差特性由(式1)可表示IMC系统的闭环偏差为：

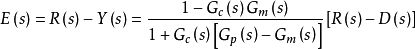
对于上式，假设满足条件，控制器的稳态增益和模型的逆是相等的，即Gc(0)=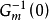 ，则可求得E ( s )=0；再由终值定理，有 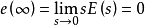，则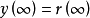 。无论对象与模型是否匹配，都能保证输出值最终稳定达到设定值，实现了系统对于常值干扰和阶跃干扰的无稳态偏差控制。这一零稳态偏差特性说明 IMC 结构本身具有积分作用，无需在控制器设计过程中引入积分项。2

理想内模控制存在问题由于实际生产条件与理论研究有较大偏差，理想的内模控制是无法实现的。比如：

(1)模型存在非最小相位部分会导致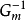 存在超前项，物理上无法实现该控制器；

(2)当模型Gm(s)严格正则时，其逆也就是理想控制器就非正则，此时控制器的微分环节会使得对于干扰异常敏感；

(3) 当模型不确定性而产生模型失配时，IMC 的控制性能都会受到极大的影响。2

内模控制器的设计方法内模控制的两步设计法能够解决完美内模控制不可实现的问题。两部设计法的基本思想是：首先，按照理想控制原则，设计出稳定的内模控制器(同时即可实现系统的闭环稳定)；然后，在控制器中加入滤波器结构；最后根据对象特性和期望的控制效果综合设定控制器的结构和相关参数。具体如下：

第一步：理想控制原则设计控制器：

先对分解过程模型Gm进行如下分解：

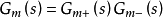
其中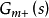， 是模型的(Non-minimum Phase, NMP)部分，且满足 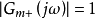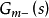； 是对象模型中最小相位部分，稳定且不包含任何预测项。

第二步：加入滤波器结构：

为了达到期望的鲁棒性和稳定性，在设计出的理想控制器中要加入滤波器结构，则内模控制器最终表达为：

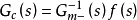
其中，f ( s )是引入的n阶滤波器，表示为：

n值的选取是要保证内模控制器Gc(s)有理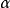； 为滤波器参数，也是IMC 结构中唯一的可用于在线调节的参数，其值大小选取是否得当会直接影响闭环系统的控制特性的优劣。2