[科普中国]-单位阶跃响应

基本概念单位阶跃函数

单位阶跃函数（Unit Step Function）属于典型输入信号，其定义为1：

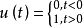
很明显的一点是，单位阶跃函数在t=0这一点是不连续的。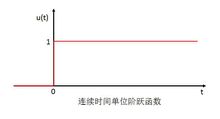

单位阶跃响应单位阶跃响应，就是指系统在接收到单位阶跃函数输入后产生的零状态响应。2

所谓零状态响应是指系统在接收到指定输入之前处于初始状态，即保证系统是完全因为指定输入（在此为单位阶跃输入）而产生的响应变化。

单位脉冲响应单位脉冲响应是指系统对单位脉冲输入的响应。单位脉冲信号是一个无穷大的瞬时冲激，表示为：

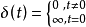
单位脉冲信号在时间上的积分是1。

对于 n 阶线性定常系统，由线性性和叠加原理，在零初值条件下，系统的单位阶跃响应函数的导数为该系统的单位脉冲响应函数。

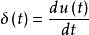
作用与意义系统动态性能分析动态性能是系统性能的一个十分重要的指标，通常用阶跃信号作用来测定系统的动态性能。

一般认为，阶跃信号对于系统来说是十分严峻的工作状态，因为阶跃信号中存在跃断点（不连续点）。

针对零初始状态系统在单位阶跃输入下的响应情况，定义了一系列动态性能指标，用以评判系统的动态性能，如超调量、衰减比、上升时间、调节时间、峰值时间等等。2

建立系统响应模型对于典型的输入信号，如冲激信号、阶跃信号、斜坡信号等，都建立有响应模型（在此即单位阶跃响应模型）。根据模型，可以快速判断出实际系统的动态性能指标参数，只需要代入实际系统的相关测量参数，就可以定量分析其性能指标。

单位阶跃响应的数学模型设单位阶跃信号r(t)=1(t)，其拉氏变换为R(t)=1/s。

一阶系统的单位阶跃响应一阶系统的传递函数为：

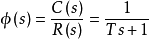
代入R(s)得到：

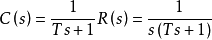
反拉氏变换：

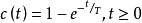
如图所示，设定时间常数T=1得到该图。

按照动态性能定义，调节时间等于3T（△=5%）或4T（△=2%）。

二阶系统的单位阶跃响应二阶系统的传递函数为：

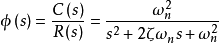
代入R(s)得到：

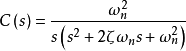
反拉氏变换：

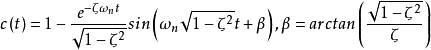
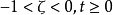
其中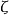 为阻尼比（相对阻尼系数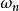）， 为自然频率（无阻尼振荡频率）。

二阶系统相比一阶系统要复杂的多，根据阻尼比和自然频率可以对系统进行分析。

一般根据阻尼比的值，分为欠阻尼、临界阻尼、过阻尼三种情况（另外也有无阻尼情况）。

高阶系统的响应情况更为复杂，一般借助计算机进行分析计算。

由单位阶跃响应求系统传递函数假设已知一个n阶线性定常系统的单位阶跃响应为c(t)，则其传递函数推导如下：

1. 首先根据c(t)得到系统的阶次，假设为n阶系统；

2. 判断c(0)、c'(0)、... 是否为0，假设c(t)在t=0处的m阶导不为0（m