[科普中国]-行阶梯形矩阵

行阶梯形矩阵，Row-Echelon Form，是指线性代数中的某一类特定形式的矩阵。1

阶梯形矩阵定义形如

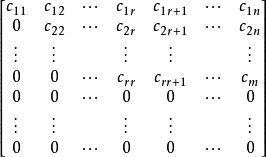的矩阵称为行阶梯形矩阵，简称阶梯型矩阵。其特点为：每个阶梯只有一行；元素不全为零的行（非零行）的第一个非零元素所在列的下标随着行标的增大而严格增大（列标一定不小于行标）；元素全为零的行（如果有的话）必在矩阵的最下面几行。1

举例例如

均为阶梯形矩阵。1

区分行最简形矩阵在阶梯形矩阵中，若非零行的第一个非零元素全是1，且非零行的第一个元素1所在列的其余元素全为零，就称该矩阵为行最简形矩阵。1

例如矩阵

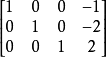
标准形矩阵在最简形矩阵中，非零行有且只有一个非零元素且为1，则称该矩阵为标准形矩阵。1

例如矩阵

矩阵变换下列三种变换称为矩阵的行初等变换：

（1）对调两行；

（2）以非零数k乘以某一行的所有元素；

（3）把某一行所有元素的k倍加到另一行对应元素上去。

将定义中的“行”换成“列”，即得到矩阵的初等列变换的定义。矩阵的初等行变换与矩阵的初等列变换，统称为矩阵的初等变换。

有如下定理成立：

（1）任一矩阵可经过有限次初等行变换化成阶梯形矩阵；

（2）任一矩阵可经过有限次初等行变换化成行最简形矩阵；

（3）矩阵在经过初等行变换化为最简形矩阵后，再经过初等列变换，还可以化为最简形矩阵，因此，任一矩阵可经过有限次初等变换化成标准形矩阵。

行阶梯形的结果并不是唯一的。例如，行阶梯形乘以一个标量系数仍然是行阶梯形。但是，可以证明一个矩阵的化简后的行阶梯形是唯一的。1

本词条内容贡献者为:

郭学军 - 教授 - 南京大学