[科普中国]-功率谱

基本简介

傅立叶级数提出后，首先在人们观测自然界中的周期现象时得到应用。19世纪末，Schuster提出用傅立叶级数的幅度平方作为函数中功率的度量，并将其命名为“周期图”（periodogram）。这是经典谱估计的最早提法，这种提法至今仍然被沿用，只不过现在是用快速傅立叶变换（FFT）来计算离散傅立叶变换（DFT），用DFT的幅度平方作为信号中功率的度量。

周期图较差的方差性能促使人们研究另外的分析方法。1927年，Yule提出用线性回归方程来模拟一个时间序列。Yule的工作实际上成了现代谱估计中最重要的方法——参数模型法谱估计的基础。

Walker利用Yule的分析方法研究了衰减正弦时间序列，得出Yule-Walker方程，可以说，Yule和Walker都是开拓自回归模型的先锋。

概念由于功率没有负值，所以功率谱曲线上的纵坐标也没有负数值，功率谱曲线所覆盖的面积在数值上等于信号的总功率（能量）。

定义功率信号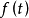 在时间段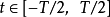 上的平均功率可以表示为

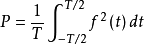
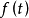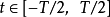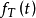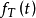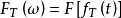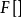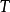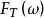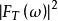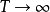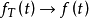如果 在时间段 上可以用 表示，且, 的傅里叶变换为 ，其中 表示傅里叶变换。当 增加时， 以及 的能量增加。当 时 ，此时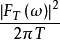 可能趋近于一极限。假如此极限存在，则其平均功率亦可以在频域表示，即

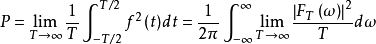
定义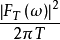 为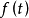 的功率密度函数，或者简称为功率谱，其表达式如下。

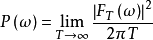
性质功率谱密度的常用性质为：2

(1)功率谱密度函数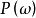 是实的；

(2)功率谱密度是非负的，即 ；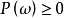

(3)功率谱密度的逆傅里叶变换是信号的自相关函数；

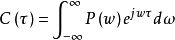
(4)功率谱密度对频率的积分给出信号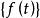 的方差，即

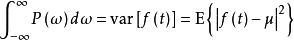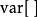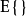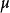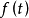上式中 表示求方差的算符， 表示求均值算符， 表示 的均值。

应用功率谱密度定义给出了区别于时域的功率描述方法，常应用于统计信号处理，介绍两个基本应用

（1）白噪声与有色噪声的定义。

若信号的功率谱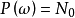 等于常数，即，则随机过程 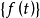称为白噪声，反之则称为有色噪声。

（2）利用其与自相关函数的关系求信号的自相关函数。

周期运动周期运动在功率谱中对应尖锋，混沌的特征是谱中出现"噪声背景"和宽锋。它是研究系统从分岔走向混沌的重要方法。 在很多实际问题中（尤其是对非线性电路的研究）常常只给出观测到的离散的时间序列X1, X2, X3,...Xn,那么如何从这些时间序列中提取前述的四种吸引子（零维不动点、一维极限环、二维环面、奇怪吸引子）的不同状态的信息呢？ 我们可以运用数学上已经严格证明的结论，即拟合。我们将N个采样值加上周期条件Xn+i=Xi，则自关联函数（即离散卷积）为 然后对Cj完成离散傅氏变换，计算傅氏系数。 Pk说明第k个频率分量对Xi的贡献，这就是功率谱的定义。当采用快速傅氏变换算法后，可直接由Xi作快速傅氏变换，得到系数 然后计算 ，由许多组{Xi}得一批{Pk'}，求平均后即趋近前面定义的功率谱Pk。 从功率谱上，四种吸引子是容易区分的，如图12 (a)，(b)对应的是周期函数，功率谱是分离的离散谱 (c)对应的是准周期函数，各频率中间的间隔分布不像(b)那样有规律。 (d)图是混沌的功率谱，表现为"噪声背景"及宽锋。 考虑到实际计算中，数据只能取有限个，谱也总以有限分辨度表示出来，从物理实验和数值计算的角度看，一个周期十分长的解和一个混沌解是难于区分的，这也正是功率谱研究的主要弊端。1