[科普中国]-克努森扩散

克努森扩散简介及有关计算

如果气体密度不大、多孔固体介质的孔径较小，则气体分子平均自由程可能远大于介质的孔径，此时气体分子与介质孔壁碰撞的机会多于分子之间的碰撞，阻止气体扩散的主要因素为气体分子与孔壁的碰撞，而分子之间的碰撞阻力可以忽略不计，我们把这种条件下的扩散称为Knudsen扩散。

根据气体分子运动学说，气体分子通过圆柱形微孔的Knudsen扩散系数Dk（cm2/s），可以按下式计算：

式中，－微孔的平均半径，cm；

－气体分子A的均方根速度，cm/s，可按下式计算：

将其代入（1）式有：

式中，MA－气体分子A的分子量；

T－绝对温度，K。

因为在低压下各种气体分子之间的碰撞可以忽略，故此式适用于体系中存在的任何组分。

如果考虑到气体分子在多孔固体介质中实际扩散截面积的较少和扩散路径的增大，则同样需要对Knudsen扩散系数进行校正：

式中，DK,E－有效Knudsen扩散系数。

对于一些在较低温度下以Knudsen扩散为主的体系，表中列出根据实验结果计算出来的曲折度。

在某些条件下，分子之间的碰撞和分子与孔壁之间的碰撞都起作用，此时总的扩散速率与分子扩散Knudsen扩散均有关系，我们把这种扩散称为混合扩散（mixed diffusion）。在这种情况下，有效扩散系数D。可以近似地表示为：1

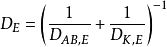
判断扩散过程以哪种扩散为主判断扩散过程是以Knudsen扩散为主，还是以分子扩散为主，通常有两种方法。

第一种方法是比较DAB和DK的大小。如果，则过程速率的限制步骤为Knudsen扩散；反之，则为分子扩散。

第二种方法是首先计算出气体分子的平均自由程：

式中，d－分子的碰撞直径，cm；

n－分子的密度，cm-3。

将计算的与孔径作比较，如果，则为分子扩散；如果，则为Knudsen扩散。1

分子扩散系数和努森扩散系数的关系应用气体动力学理论，可以导出下式：

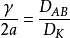
式中，A－分子的平均自由程，cm。

该式表明，γ对2a的比值等于分子扩散系数DAB和努森扩散系数DK之比。由此可以确定在某一扩散过程中，是否可以忽略分子扩散系数式或努森扩散系数。很明显，在压力或分子浓度上升时，将发生从努森扩散向分子扩散的转化。2