[科普中国]-电磁透镜

概念

电子作为带电粒子在磁场中运动会受到洛伦兹力的作用，轴旋转对称磁场可以使运动着的电子折射而发生“聚焦”，像可见光通过玻璃透镜一样用来成像。用电磁线圈可以产生轴旋转对称磁场，把这种能对运动电子聚焦成像的装置称为“电磁透镜”或“磁透镜”。

图1-1所示的通电短线圈就是一个简单的电磁透镜，磁感应强度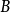 由电流方向决定。

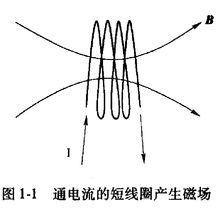
图1-2是电磁透镜聚焦原理示意图。磁透镜造成一种轴对称不均匀分布的磁场，磁力线围绕导线呈环状，磁力线上任意一点的磁感应强度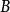 都可以分解成平行于透镜主轴的分量 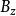和垂直于主轴的分量 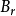。速度为 平行于透镜主轴的电子进入透镜的磁场时，位于透镜上半部Ⅰ点的电子受到垂直分量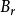 的作用，使电子受到切向力。根据左手法则，电子所受的切向力 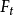的方向如图1-2所示。

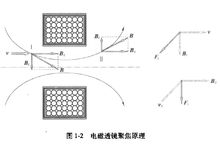
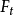使电子获得切向速度 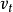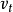， 随即和 分量叉乘，形成了另一个向透镜主轴靠近的径向力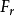 ，使电子向主轴偏转。平行入射到磁场中的电子到达不同的位置，都得到切向速度 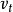使电子做圆周运动，同时都具有轴向速度 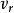使电子趋向轴上的一点。当电子穿过线圈运动到透镜的下半部Ⅱ点位置时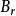， 的方向改变了180°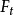， 随之反向，但是 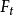的反向只能使 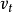变小，而不能改变其方向。因此穿过线圈的电子仍然向主轴靠近。电子的运动轨迹是原来平行于主轴的直线运动、圆周运动和向轴运动的合运动，整体轨迹是圆锥螺旋状，最终落到磁透镜的轴上，完成电子的磁聚焦。

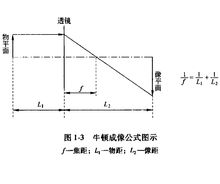
一束平行于主轴的入射电子束通过电磁透镜时被聚焦在轴线上一点，这一点称为焦点，这与光学玻璃凸透镜对平行于透镜主轴入射的平行光的聚焦作用十分相似，仍可用牛顿成像公式来说明这一聚焦过程。见图1-3。1

电磁透镜的像差按照衍射理论计算结果，光学透镜的分辨率是波长的一半。对于电磁透镜来说，目前还远远没有达到这一水平。主要原因是除了衍射效应对分辨率的影响外，还有像差对分辨率的影响。电磁透镜的主要像差有球差、像散和色差。

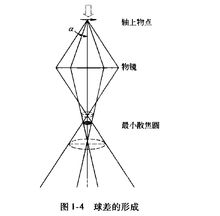
球差球差是由电磁透镜近轴区域磁场和远轴区域磁场对电子束的折射能力不同而产生的像差。近轴区域对电子束的折射能力弱，远轴区域对电子束的折射能力强。来自于轴上物点散射的电子束，经过电磁透镜折射后到达像平面本应该形成一个对应的像点，但实际上近轴电子和远轴电子不聚焦在同一点上（图1-4），这种由于透镜磁场折射能力不同形成的像点发散就是球差。像平面上沿轴线从远轴电子聚焦点到近轴聚焦点之间，存在一个像平面，其上的散焦斑最小，同其他各处的圆斑相比，这个散焦斑最清晰，就把最小散焦斑作为与物点对应的像点。设散焦斑半径为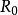 ，将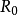 除以放大倍数 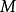把最小散焦斑折算到物平面上，有 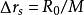，原来的物点由于球差的影响变成了半径为 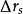的漫散圆斑，用 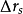表示球差大小，按照物理光学的相关公式，有：

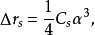式中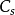， 为球差系数，通常情况下电磁透镜的球差系数 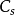相当于它的焦距，大小约为1~3mm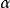； 为孔径半角。由上式可见，减小球差系数和孔径半角可以减小球差，尤其是孔径半角减小时，球差显著减小。

球差是影响电磁透镜分辨率的主要像差，它不能像光学透镜那样通过设计凸透镜、凹透镜的组合来补偿消除。但最近发明的电磁透镜球差矫正器可以有效地降低球差系数。

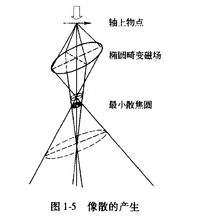
像散像散是由透镜磁场的非旋转对称引起的像差。透镜的极靴孔加工误差，上、下极靴的轴线错位、极靴材质不均以及极靴孔周围的局部污染等，都会引起透镜的磁场产生椭圆度。椭圆磁场长、短轴方向上的聚焦能力存在差异，结果成像物点通过透镜后不能在像平面上聚焦于一点（图1-5）。

同样在长、短轴聚焦点之间有一个最佳聚焦位置，此处像平面上得到一个最小散焦斑，半径为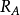 ，将 折算到物平面上得到一个半径为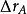 的漫散圆斑，用 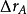表示像散的大小，其计算公式为：

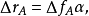式中， 为像散系数，等于磁透镜出现椭圆度时造成的焦距差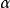； 为孔径半角。电磁透镜的像散是可以消除的像差，通常引入一个强度和方位可调的矫正磁场来进行补偿，产生这个矫正磁场的装置称为消像散器。

色差色差是由于成像电子的能量不同或波动，电子在透镜磁场中运动速度不同，从物面上一点散射的电子不能聚焦在像面上同一点而形成的像差，如图1-6所示。

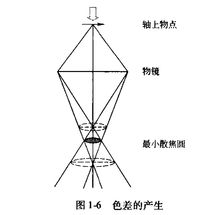
不同能量的电子聚焦在不同位置，像平面上也有一个最小半径为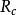 的散焦斑。同样将 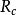折算到物平面上，得到半径为 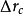的圆斑，用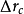 表示色差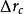， 的大小由下式来确定：

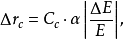式中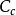， 是电磁透镜的色差系数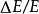； 是电子束的能量变化率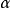； 为孔径半角。上式说明，在色差系数和孔径半角一定的情况下，电子能量的波动是主要影响因素。引起电子能量波动的原因主要有两个：一是电子加速电压不稳，致使入射电子能量波动；二是电子束照射试样时和试样相互作用，部分电子产生非弹性散射，致使能量变化。1

电磁透镜的景深和焦长景深透镜的景深是指当像平面固定时（像距不变），在保持图像清晰的条件下，允许物平面（样品）沿透镜主轴平移的最大距离。

在理想状态下（不考虑衍射差、球差、像散和色差等影响），由图1-7可见样品上某一物点位于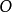 位置时，该点在像平面上应形成一个像点 。

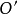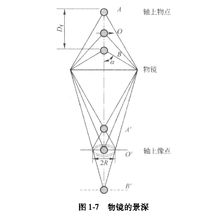
当试样向上方移动，使O点到达A点时，A点的像应位于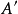 处。如果像平面的位置保持不变，则 点将在像平面上散焦成一个半径为R的圆斑；当试样向下移动，使原物点O到达B点时，B点将在像平面的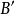 处成像，同样会形成一个半径为R的散焦斑。

如果衍射效应是决定透镜分辨率的控制因素（即上述诸因素中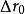 为最大），在像平面上由衍射引起的散焦斑半径应是 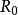，因此，只要物点在像平面上形成的圆斑半径R小于或等于 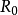时，像平面上的图像就仍能保持清晰，所以，样品在从A到B的范围内移动时，并不影响物像的清晰度，AB间的这段距离称为景深，用 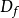表示。

由图1-7的几何关系可知：

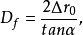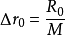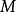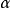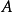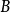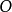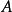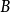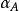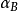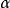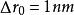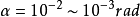式中， ， 为放大倍数； 为孔径半角。因为电磁透镜的孔径半角很小，同时 、 两点间的距离比透镜的物距小得多，所以可以认为样品上的物点 在位于位置 和位置 时，相应的 、 近似地和 相等。如果 ， ，求出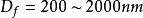 。透射电子显微镜的金属薄膜试样的厚度一般只有 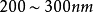，因此上述景深范围可以保证样品整个厚度范围内各处细节都清晰可见。

焦长透镜的焦长是指固定样品的条件下（物距不变），像平面沿透镜主轴平移时仍能保持图像清晰的最大距离。

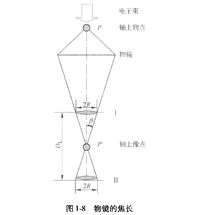
由图1-8可见，样品上某一点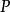 通过透镜后正焦位置应是 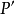点。如果把像平面移动到Ⅰ位置，则 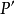点将散焦成一个半径为 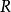的欠焦斑；如果把像平面反向移动相等的距离到达位置Ⅱ时，则得到半径为 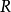的过焦斑。若决定透镜分辨率的控制因素仍是衍射效应，由衍射产生的最小散焦斑直径等于 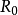，在物平面上为 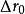，则根据图1-8中的几何关系可以得到：

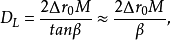
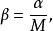
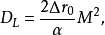式中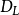， 就是透镜的焦长。如果 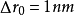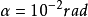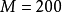， ， 倍，则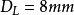 。考虑到电子显微镜是多级放大，总放大倍数可以很高，如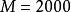倍时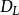，可达到80cm。这使得在透射电镜中，荧光屏和照相底片之间的距离可以很大，只要在焦长范围内就能得到清晰的图像。

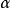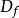从计算景深和焦长的公式中可以看到，随着孔径半角的减小，和都会变大，因此，在电磁透镜中插入一个直径较小的光阑时，可明显增加景深和焦长。1