[科普中国]-二进制信道

信道是信息传输的通道，即信息进行传输时所经过的一条通路。一条传输介质上可以有多条信道（多路复用）。与信号分类相对应，信道可以分为用来传输数字信号的数字信道和用来传输模拟数据的模拟信道。数字信号经过数——模转换后可以在模拟信道上传输；模拟信号经过模——数转换后可以在数字信道上传输。

二进制信道是仅使用1，0两种符号的任何信道，属于数字信道的一种。

分类BSC二进制对称信道（Binary Symmetric Channel）是离散无记忆信道（discrete memoryless channel）在J=K=2时的特例。

它的输入和输出都只有0和1两种符号，并且发送0而接收到1，以及发送1而收到0（即误码）的概率相同，所以称信道是对称的。此时条件差错概率（conditional probability）由p表示。二进制对称信道的转移概率如图1。

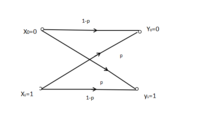
定义

一个二进制对称信道与交叉概率p记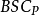 ，与二进制输入和二进制输出和错误的概率渠道p;即，如果X是发射随机变量和Y接收变量，则该信道的特征在于，条件概率

PR（Y= 0 |X= 0）= 1 -p

PR（Y= 0 |X= 1）=p

PR（Y= 1 |X= 0）=p

PR（Y= 1 |X= 1）= 1 -p2

假定0≤p≤1/2。如果p> 1/2，则接收机可以交换输出（解释1，当它看到0，反之亦然），并获得与交叉概率1的等效信道-p≤1/2

BSC的容量

该信道的容量是1 - H（p），其中H（p）是二进制熵函数。

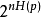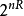可以通过一个球体包装参数显示。给定一个码字，有大约 典型的输出序列。有 个可能总输出和输入选择从码本的大小 。因此，接收器会选择分区的空间为 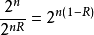的潜在输出。当R>1−H（P），则球将被太紧密包装，接收器将无法识别正确的码字与消失的概率。1

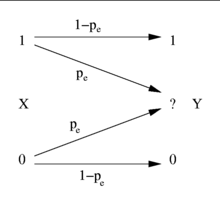
BEC二进制删除信道（Binary Erasure Channel）又被称为二进制擦除信道，BEC是二元通道，即它只能传输一个符号（通常称为0和1）。（一个非二进制信道将能够传输两个以上的符号，甚至可能是一个无限数量的选择）信道是不完美的，有时会被“删除”。

BEC，在某种意义上来说是无错误。不同于二进制对称信道，当接收机得到一个位，它是100%确定的位是正确的。只有当位被擦除时，才会出现唯一的混淆。

X是所发送的随机变量与字母表{0，1}。让Y与字母所接收的变量{0,1，ê}，其中ê是擦除符号。

信道的特征是条件概率。

二进制删除信道的信道模型显示一个映射从通道输入X到通道输出Y（与已知的擦除符号？），删除的概率是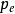 .1

BEC的容量

BEC的容量是1- 。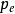

直观地说1 -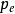 可以被看作是一个上限的信道容量。PE可以被看作是对信道容量的上限。假设有一个无所不知的“精灵”，告诉每当发送位被擦除时它的来源。没有什么来源可以做，以避免删除，当他们发生时它可以解决这些问题。例如，它得到通过源可以重复发送一个位。不需要X码，Y根本不理会擦除，知道下一个成功接收点是X寄意。因此，有一个精灵使我们能够达到1 - Pe的平均水平。此额外的信息是不正常的，因此1 - 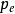是一个上限。

信道删除二进制删除信道不应删除信道从发射机位被传送到接收器混淆（以概率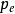 ）或下降不通知接收器（以概率1- 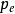）。确定删除信道的熵是一个悬而未决的问题。